基本图形分析法：角平分线和平行线的组合图形

【分析方法导引】

当几何问题中出现角平分线和平行线的组合关系式，就可以想到要应用等腰三角形的基本图形进行证明。然后就应用将角的边的平行线与角平分线及角的另一边相交或将角平分线的平行线与角的一边及另一边的反向延长线相交的方法找到等腰三角形的基本图形。再应用角平分线、平行线、等腰三角形中任何两个性质成立就可以推得第三个性质成立的方法来完成分析。

例13 如图3-40，已知：△ABC中，AD是角平分线，M是BC的中点，MF∥DA交AB和CA的延长线于E、F。求证：BE=CF=1/2（AB+AC）。

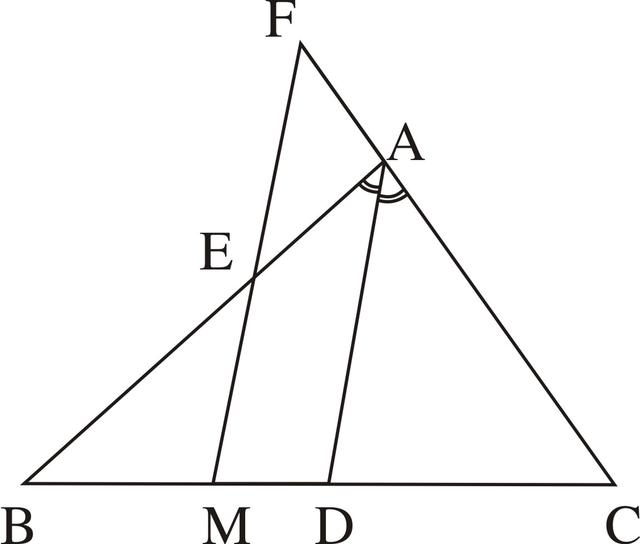
图3-40

分析：本题的条件中出现了AD是角平分线，MF∥DA，构成了角平分线和平行线的组合关系，所以可得到一个等腰三角形的基本图形，由于MF是角平分线的平行线，所以它应和角的一边（AB）以及另一边（AC）的反向延长线相交构成等腰三角形，于是就可以找到这个等腰三角形应是△AEF（如图3-41），于是由∠EAD=∠CAD和MF∥DA，∠AEF=∠EAD，∠F=∠CAD，可得∠AEF=∠F，AE=AF。

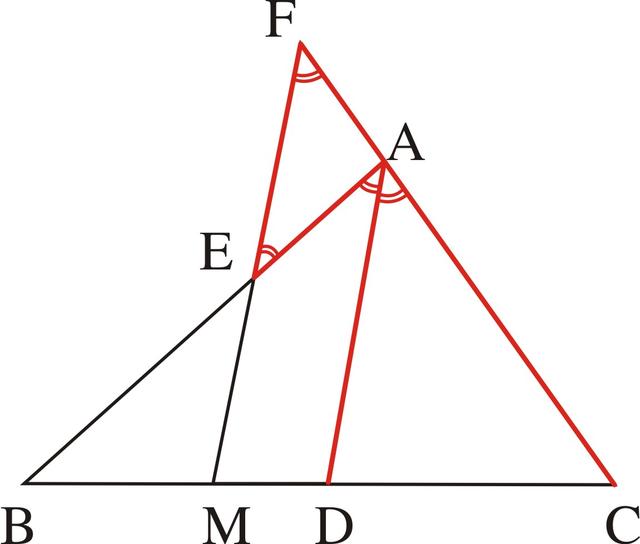
图3-41

由于AF是结论中出现的线段CF的一部分，这样AF就可以看作是折过来成为AE，所以CF就转化成CA+AF=CA+AE，问题就成为要证BE=CA+AE。

现在出现的问题就是要证明一条线段等于两条线段的和，所以可根据线段和的定义将两条线段接起来，或者也就是将其中的一条线段接到另一条线段上去。但将AE接到CA上，则问题又回到了原来的性质，所以只能考虑将AC接到EA上，即延长BA到G使AG=AC（如图3-42），于是要证的结论又进一步化为BE=CA+AE=AG+AE=EG，即要证E是BG的中点。

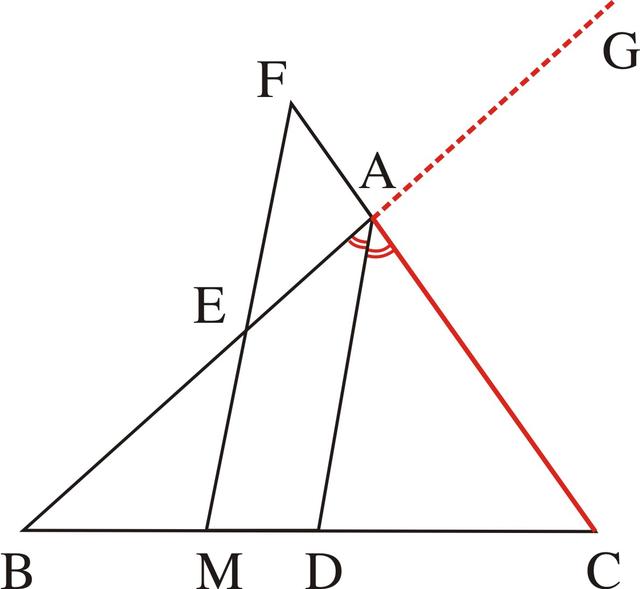
图3-42

又因为在作了AG=AC后，这就是两条具有公共端点的相等线段，它们就可以组成一个等腰三角形，但这个等腰三角形只有两条腰而没有底边，所以应考虑将底边添上，于是连接CG（如图3-43）。又因为条件中出现AD是角平分线，从而在这里又出现了一次等腰三角形和角平分线的组合关系，所以必定会出现一个平行线的基本图形，也就是由AD是等腰△ACG的顶角的外角平分线，就可推得AD∥GC。也就是由AC=AG和B、A、G成一直线，可得∠ACG=∠G，∠BAC=ACG+∠G=2∠G，又因为∠BAC=2∠BAD，从而就可得∠BAD=∠G和AD∥GC。又因为已知ME∥DA，所以又有GC∥EM。

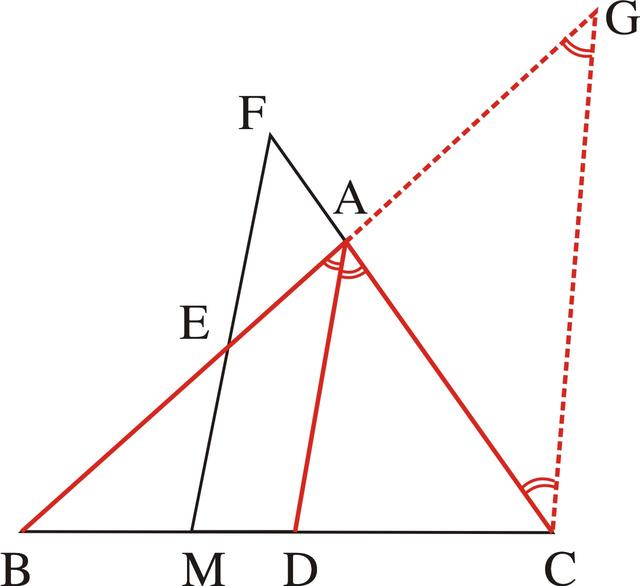
图3-43

最后就可以由BM=CM和ME∥CG，再应用三角形中位线的基本图形性质来证明BE=EG。

而在证明BE=EG=CF后，就可进一步得到BE=1/2BG=1/2（AB+AG）=1/2（AB+AC）。

本题在由AD是角平分线和MF是DA的平行线得到应添加等腰三角形的基本图形进行证明以后，由于MF是角平分线的平行线，所以它也可以和角的一边以及角的另一边的平行线相交构成等腰三角形，由于它已和角的一边AB相交于E，所以它应和AC的平行线相交，而图形中尚没有AC的平行线，所以应先将这条平行线添出。

若考虑过端点B作AC的平行线，则过B作BG∥AC交FM的延长线于G（如图3-44），那就可得△BGE应是等腰三角形。也就是可由GF∥DA，得∠BEG=∠BAD，由BG∥AC，得∠G=∠F，而∠F=∠CAD，∠CAD=∠BAD，所以∠BEG=∠G，BE=BG，这样问题就可以转化为证BG=CF。

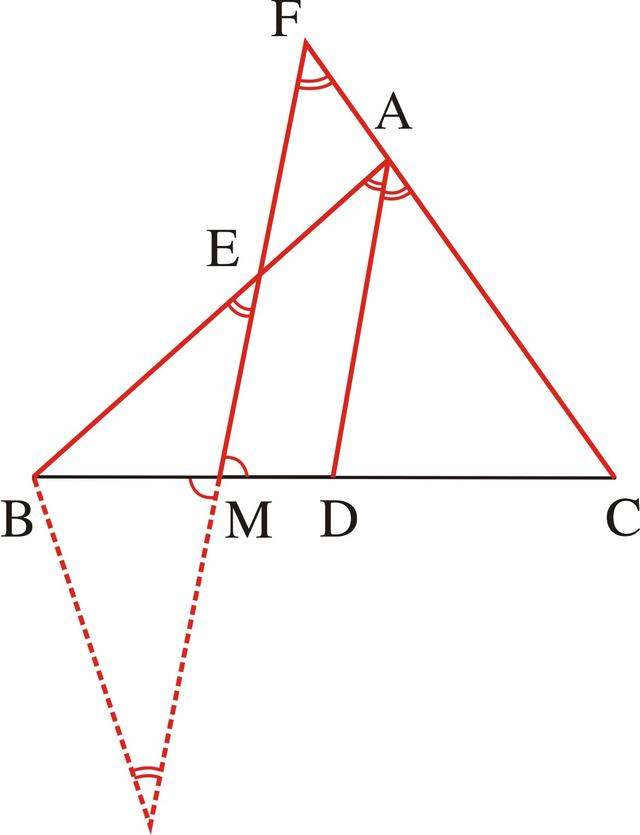
图3-44

由条件BM=CM，且BC、FG在M点相交，就出现了两条相等的线段在一组对顶角的两边，而且成一直线，所以可应用中心对称型全等三角形来进行证明（如图3-45），由BM=CM、∠BMG=∠CMF和∠G=∠F，就可以证明△BMG≌△CMF，即可证得BG=CF。

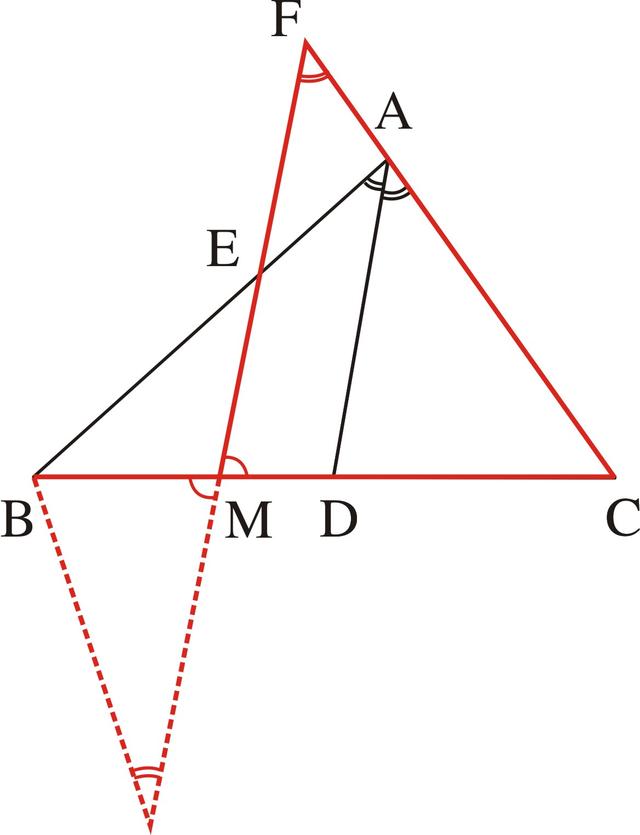
图3-45

再进一步可得AB+AC=BE+EA+AC。而在前述分析中已经证明了EA=FA，所以AB+AC=BE+FA+AC=BE+CF=BE+BE=2BE，从而也就可证明BE=CF=1/2（AB+AC）。

若考虑过中点M作AC的平行线，则过M作MG∥CA交AB于G（如图3-46），那么△GME就应是一个等腰三角形，也就是由MF∥DA和∠BAD=∠CAD，可得∠GEM=∠GAD，∠GME=∠F=∠CAD，并进而得∠GEM=∠GME，GM=GE。

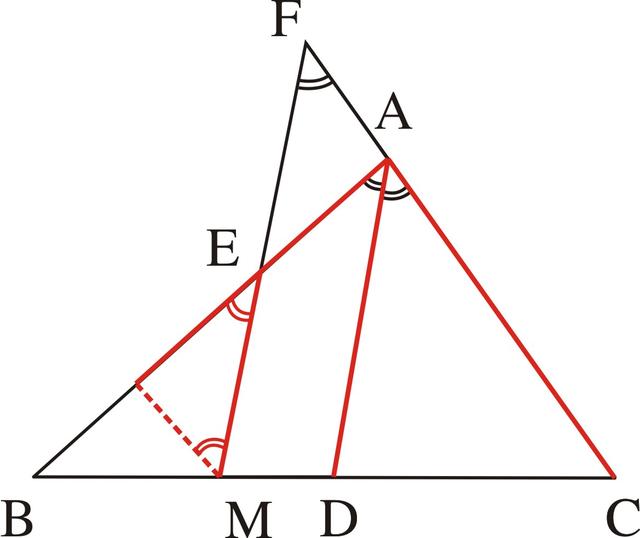
图3-46

但由BM=CM，MG∥CA，就可应用三角形中位线的基本图形性质得BG=AG=1/2AB，GM=1/2AC。于是就有BE=BG+GE=1/2AB+GM=1/2AB+1/2AC=1/2（AB+AC）。

而CF=AC+AF=AC+AE=AC+（AG-EG）=AC+1/2AB-1/2AC=1/2（AB+AC），所以分析可以完成。

在上述分析中，由于出现了MG是角的一边CA的平行线，所以这条平行线也可以与角的另一边以及角平分线相交构成等腰三角形，于是过M作AC的平行线交AB于G，交AD的延长线于H（如图3-47），这样就可得GH=GA，接下来的分析可请读者自行完成。

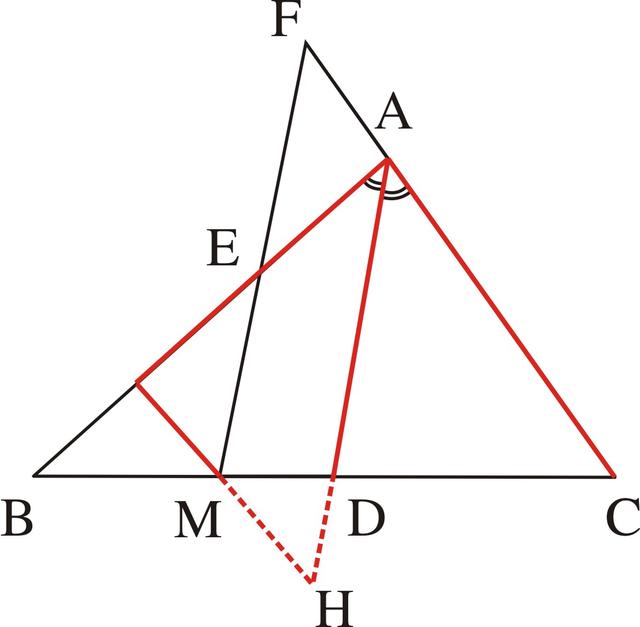
图3-47

例14 如图3-48，已知：△ABC中，AD是角平分线，CE∥DA交BA的延长线于E，F是CE的中点。求证：FA⊥DA。

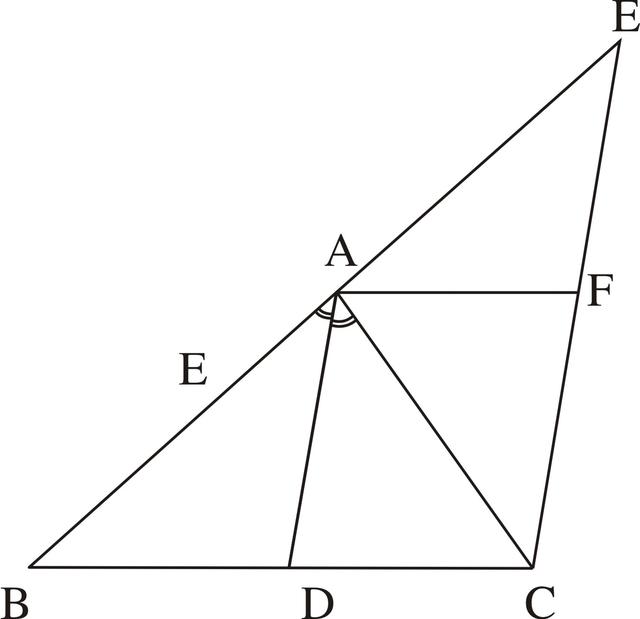
图3-48

分析：本题条件中出现了AD是角平分线和CE∥DA，是一个角平分线和平行线的组合问题，所以就可以得到一个等腰三角形的基本图形（如图3-49）。由于CE是角平分线DA的平行线，所以它应和角的一边AC以及另一边AB的反向延长线相交组成等腰三角形，于是即可找到这个三角形应是△ACE，也就是由∠BAD=∠CAD，CE∥DA，可得∠ACE=∠CAD，∠E=∠BAD，∠ACE=∠E，AC=AE。

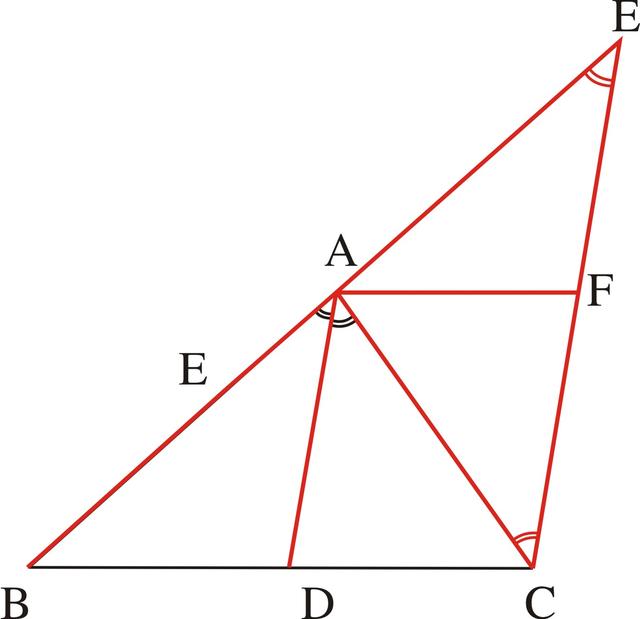
图3-49

在证明了AC=AE后，再由条件F是CE的中点，出现了AF是等腰三角形底边上的中线，所以应用等腰三角形中的重要线段的基本图形的性质，就可得AF⊥CE，而CE∥DA，所以AF⊥AD就可以证明。