初三模拟考试中题目第一问会做，第二问竟然不会做

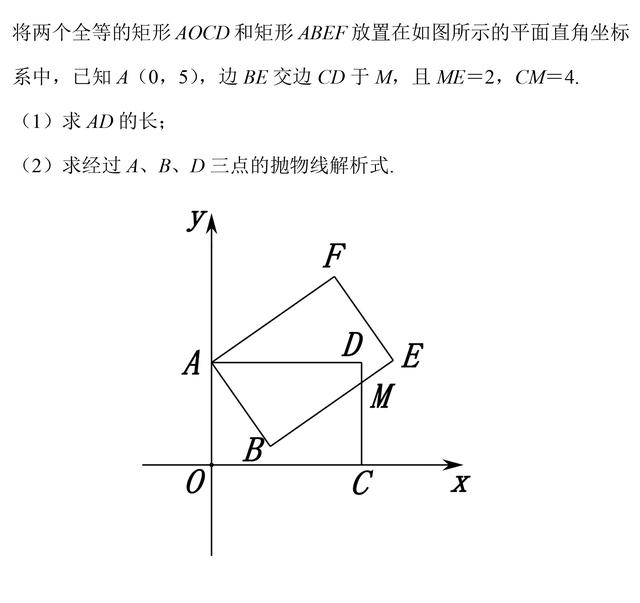
（1）如图①，连接AM，设OC＝AD＝m，

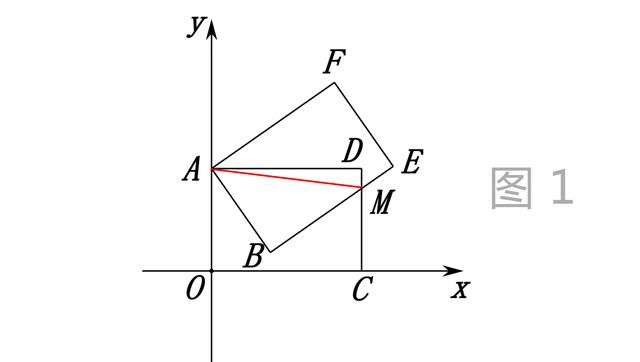
图1

根据已知条件可知，AB＝CD＝OA＝5，BE＝OC＝m，

所以，BM＝m－2，DM＝1，

因为AB²＋BM²＝AD²＋DM²

所以5²＋（m－2）²＝m²＋1²，求得m＝7，即AD＝7；

（2）如图②，过点B作x轴的平行线GH，交OA、CD于G、N，

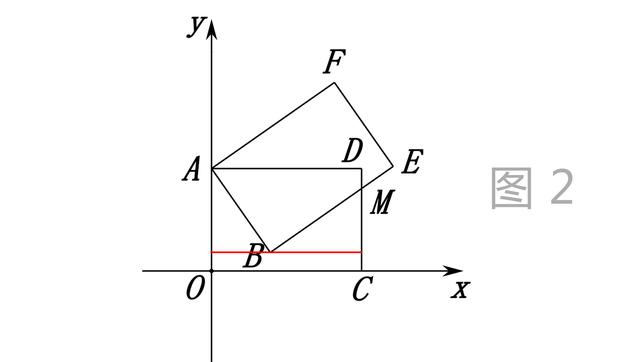
图2

由（1）可知AB＝BM＝5，

易证△ABG≌△BMH，

设G（0，n），

则HC＝OG＝n，所以GB＝MH＝4－n，BH＝AG＝5－n，因为GH＝GB＋BH＝9－2n，GH＝OC＝7，

所以n＝1，所以B（3，1）

又因为D（7，5），从而抛物线为y＝x²/3－7x/3＋5.