需要用“相似”来解决的图形 “形状” 如下:
一、“A” 字型:
1、如图、在△ABC中,DE∥BC ,分别交 AB、AC 于点 D ,E 。若 AD = 3 ,DB = 2 ,BC = 6 ,则 DE 的长为?
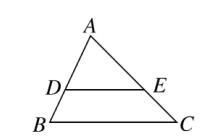
图(1)
解:△ADE∽△ABC; AD : AB = DE : BC ; 3 : 5 = DE : 6 ; DE = 18/5 。
2、如图、在Rt△ABC 中,AB = BC , ∠B = 90° ,AC = 10√2 。四边形BDEF 是△ABC的内接正方形(点 D、E、F在三角形的边上)。则此正方形的面积是多少?
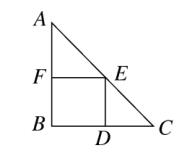
图(2)
解:

图(3)
3、如图、棱形ABCD的边长为 1 ,直线 l 过点 C ,交 AB 的延长线于点 M ,交 AD 的延长线于点 N 。
则 1/ AM + 1/AN = ?
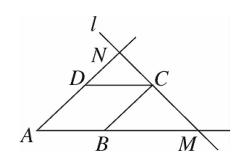
图(4)
解:

图(5)
二、“X” 字型:
4、如图、四边形ABCD 是平行四边形,则图中与△DEF 相似的三角形共有多少个?
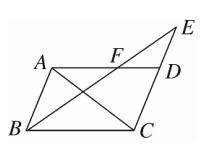
图(6)
解: “X” 字型: △ABF ∽ △DEF ; “A” 字型: △CEB ∽ △DEF 。
故图中与△DEF 相似的三角形共有 2 个。
三、“旋转” 型:
5、如图、在△ABC中,∠ACB = 90°,∠A = 30°,将△ABC 绕点 C 顺时针旋转得到 △A'B'C ,点 B‘ 在AB 上,
A'B' 交 AC 与 F ,则图中与 △AB'F 相似的三角形有多少个?(不要添加其它线段)
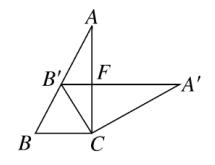
图(7)
答案: 共有 4 个 。
四、“垂直” 型:
6、如图、在△ABC 中,∠ACB = 90° ,CD⊥ AB 于点 D ,则图中相似三角形共有几对?
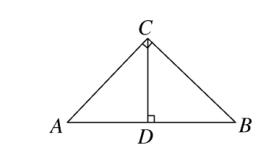
图(8)
答案:共有 3 对 。 (两小相似、两小和一大分别相似 ,由此可证“ 射影定理”。)
7、如图、矩形ABCD 中,M 是 BC 边上且与 B、C 不重合的点,点 P 是射线 AM 上的点 ,若以 A、P、D为顶点的三角形与 △ABM 相似 ,则这样的点共有多少个?
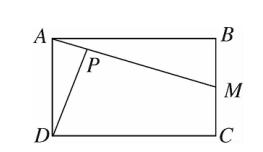
图(9)
解:

图(10)
8、如图、将长为 16 cm ,宽为 8 cm 的矩形纸片 ABCD 折叠,使点 A 和点 C 重合,则折痕 EF 的长是多少?
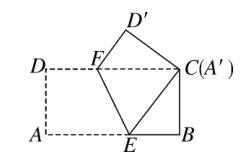
图(11)
解:

图(12)
五、“一线三等角” 型:
9、如图、AB⊥BD ,ED⊥CD ,C 是线段 BD 的中点,且 AC⊥CE ,ED = 1 ,BD = 4 , 则 AB = ?
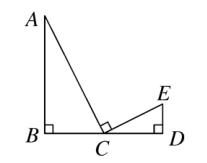
图(13)
答案: AB = 4 。
10、如图、在边长为 9 的正三角 ABC 中, BD = 3 ,∠ADE = 60° ,则 AE 的长为?
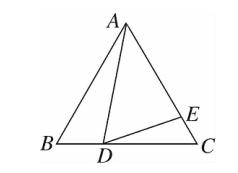
图(14)
解:“一线”:线段BC 、“三等角”:∠B = ∠ADC = ∠C 、结论: △ABD ∽△DCE 。

图(15)
 加载中,请稍侯......
加载中,请稍侯......
精彩评论