中考数学，专题复习72：与圆有关的几何证明题

典型例题分析1：

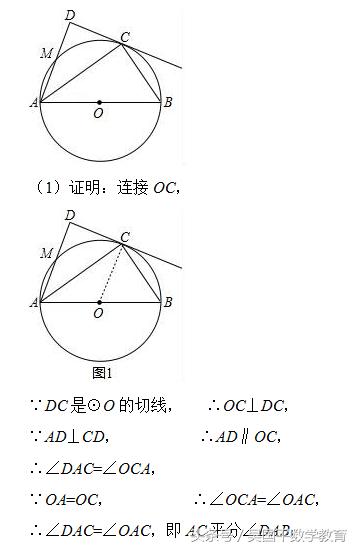
如图，⊙O的直径AB长为12，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．

（1）求证：AC平分∠DAB．

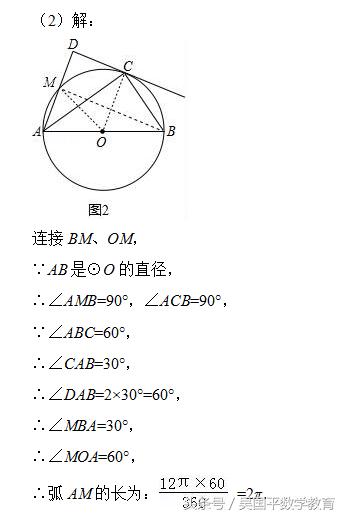
（2）设AD交⊙O于点M，当∠B=60°时，求弧AM的长．

考点分析：

切线的性质；弧长的计算．

题干分析：

（1）连接OC，根据切线性质求出OC⊥CD，根据平行线的判定得出AD∥OC，即可求出答案；

（2）连接BM和OM，求出∠AOM的度数，根据弧长公式求出即可．

典型例题分析2：

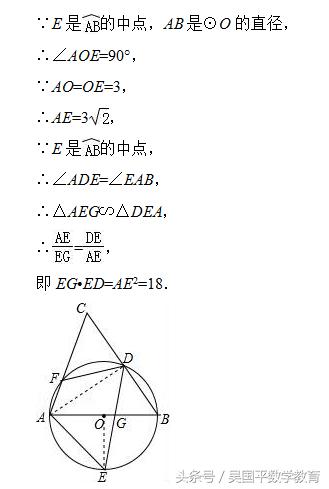
如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD，连接AC交⊙O于点F，连接AE、DE、DF．

（1）证明：∠E=∠C；

（2）若∠E=55°，求∠BDF的度数；

（3）设DE交AB于点G，若DF=4，cosB=2/3，E是弧AB的中点，求EG•ED的值．

考点分析：

圆的综合题．

题干分析：

（1）直接利用圆周角定理得出AD⊥BC，再利用线段垂直平分线的性质得出AB=AC，即可得出∠E=∠C；

（2）利用圆内接四边形的性质得出∠AFD=180°﹣∠E，进而得出∠BDF=∠C+∠CFD，即可得出答案；

（3）根据cosB=2/3，得出AB的长，即可求出AE的长，再判断△AEG∽△DEA，求出EG•ED的值．