学习目标：倍角问题、中点问题、线段的和差问题
在几何证明巧添辅助线，目的有三：
①通过添加辅助线，使图形的性质由隐蔽得以显现，从而利用有关性质去解题；
②通过添加辅助线，使分散的条件得以集中，从而利用它们的相互关系解题；
③把新问题转化为已经解决过的旧问题加以解决。
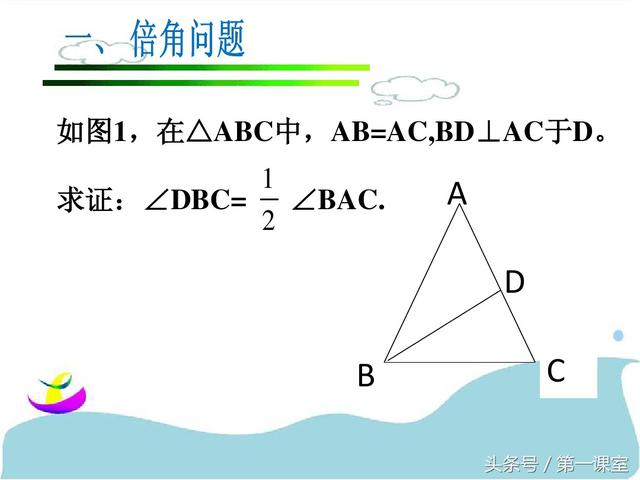
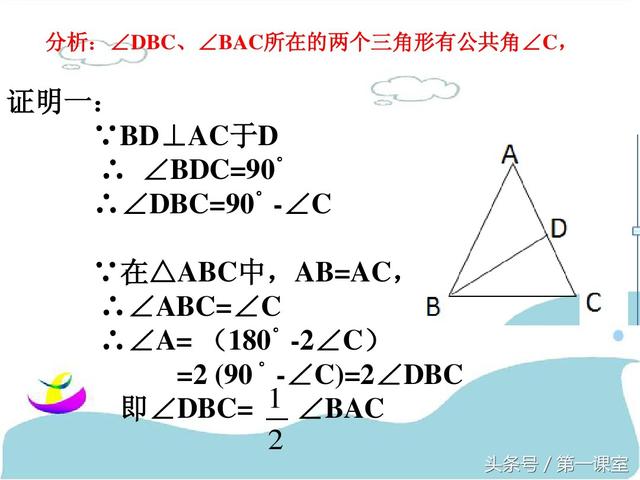
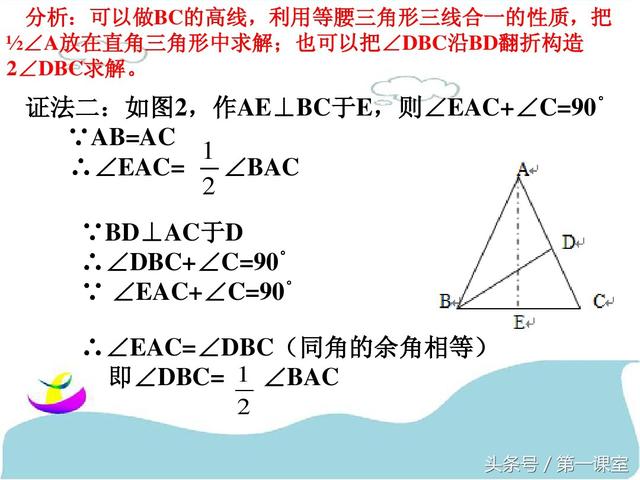
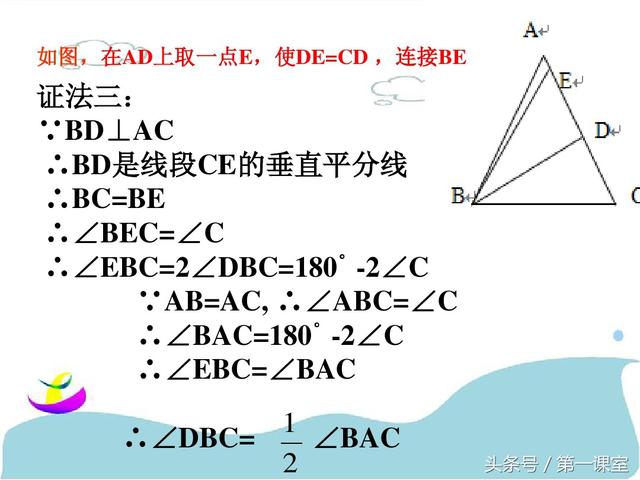
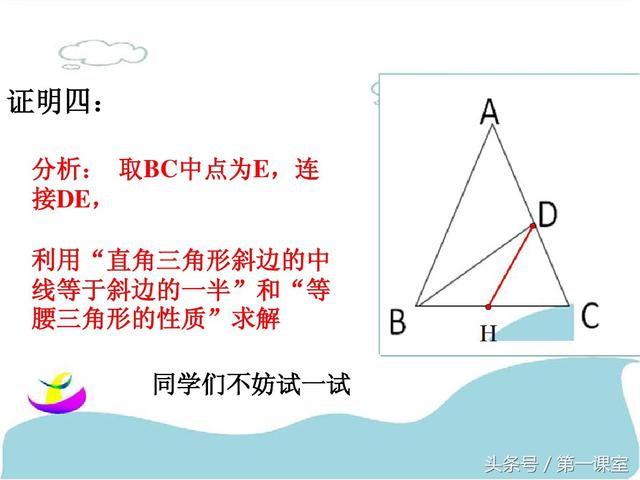
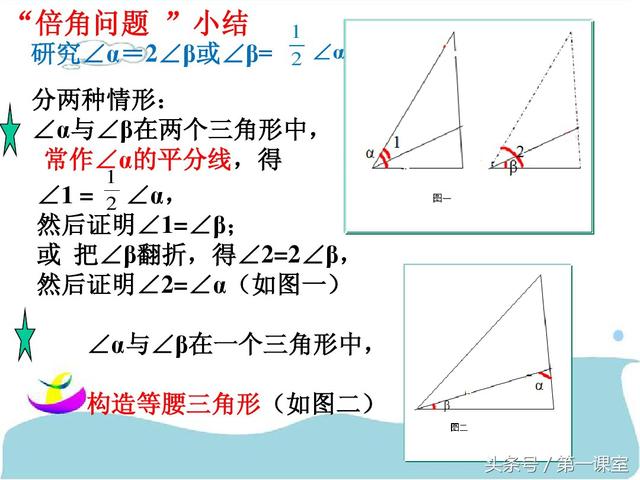
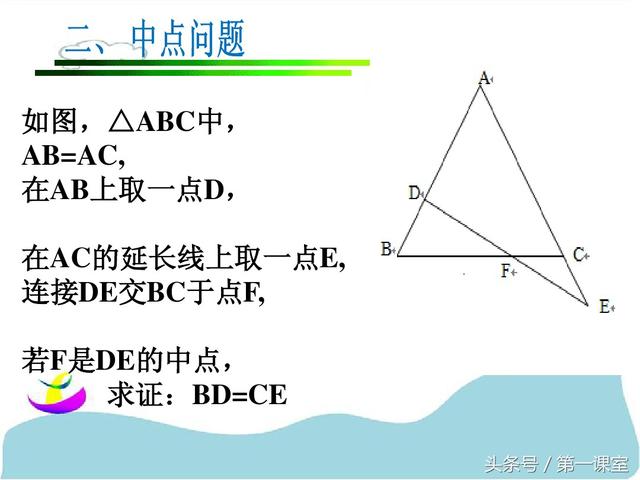
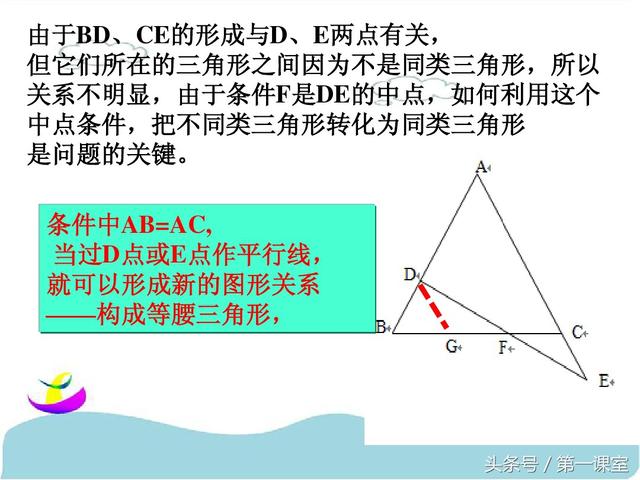
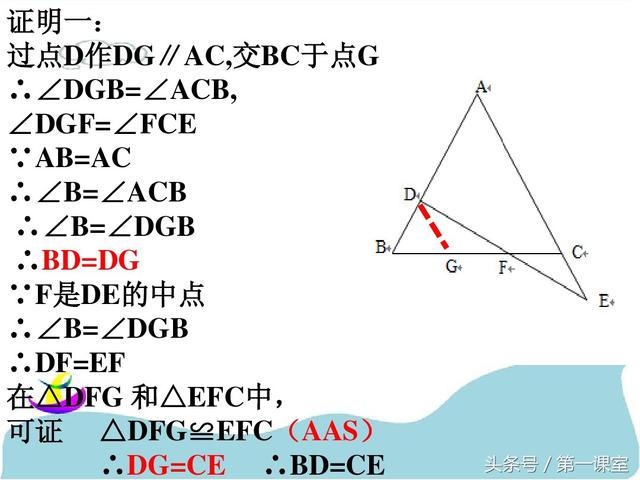
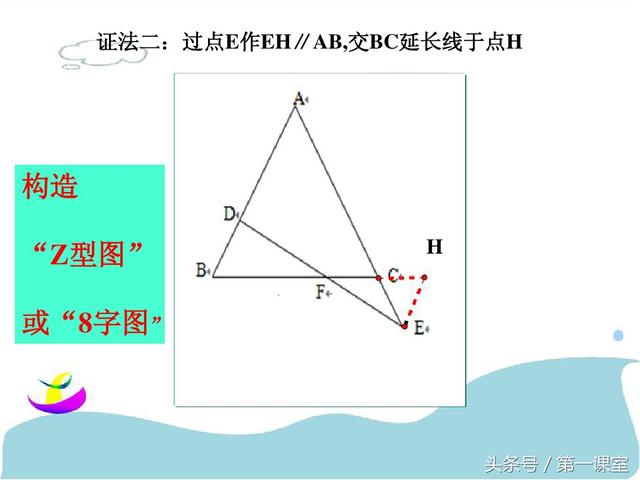
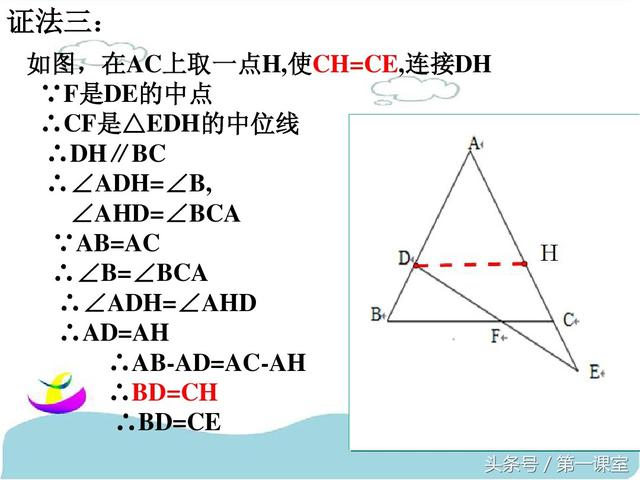
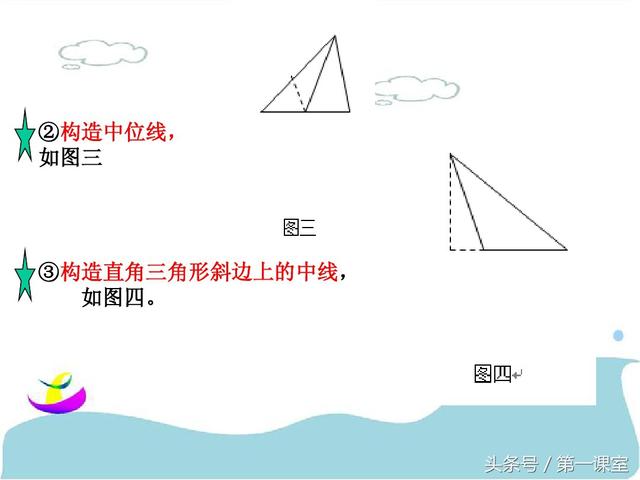
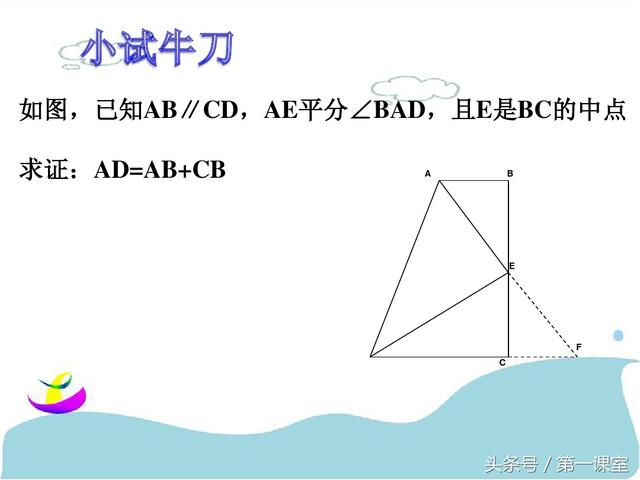
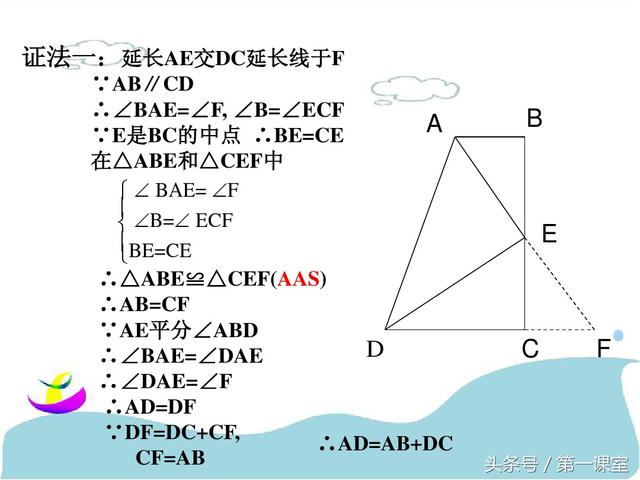
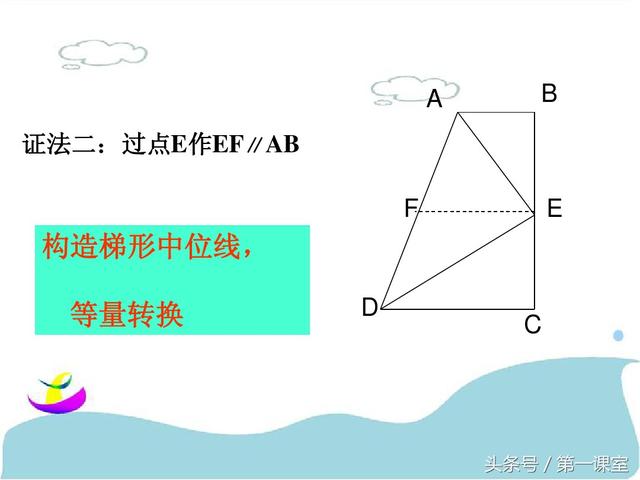
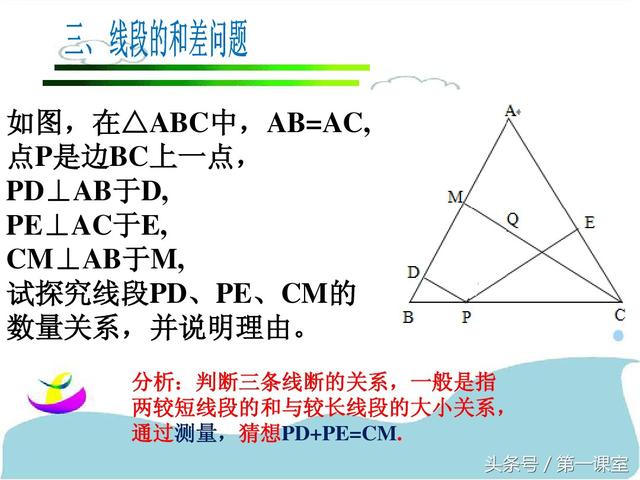
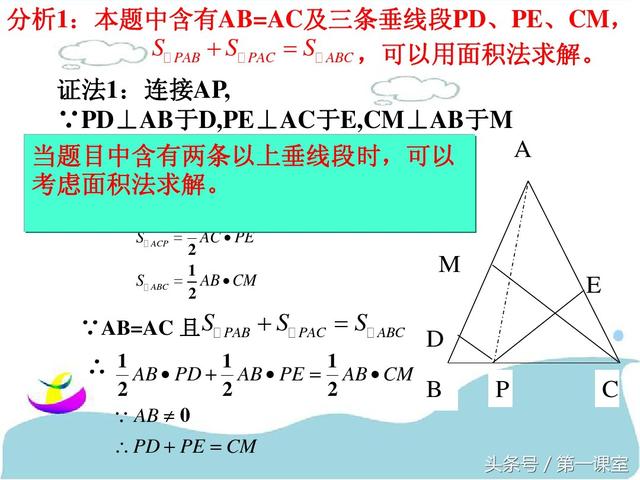
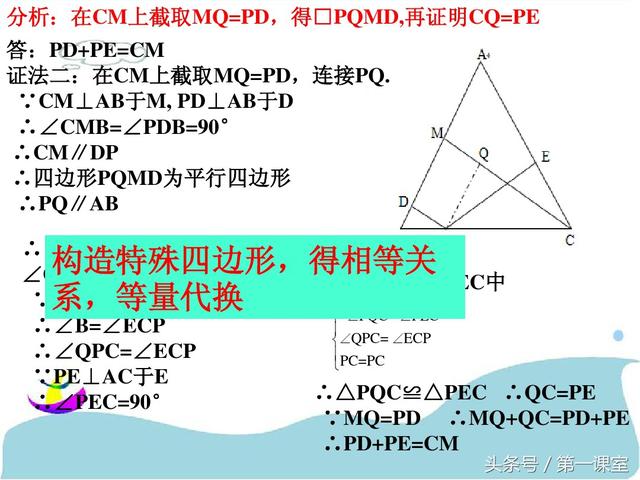
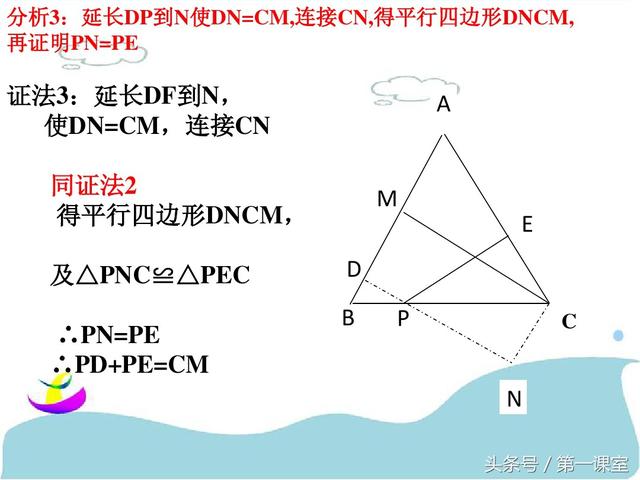
巧作数学辅助线：一题多解在几何证明中的应用
巧作数学辅助线：一题多解在几何证明中的应用
提示：键盘也能翻页，试试"← →"键
上一篇 : 初中数学专题：中点坐标公式在平行四边形存在性问题中的应用
下一篇 : 八年级尖子生培养数学试题（因式分解）
加载中,请稍侯......
精彩评论