高考必考点：圆锥曲线综合应用

一、基础知识

1、直线与圆锥曲线的位置关系

判断直线l与圆锥曲线C的位置关系时,通常将直线l的方程Ax+By+C=0(A,B不同时为0)代入圆锥曲线C的方程F(x,y)=0,消去y(或x)得到一个关于变量x(或y)的一元二次方程.

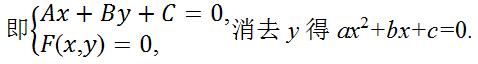
(1)当a≠0时,设一元二次方程ax^2+bx+c=0的判别式为Δ,

则Δ>0⇔直线与圆锥曲线C相交;

Δ=0⇔直线与圆锥曲线C相切;

Δ<0⇔直线与圆锥曲线C相离.

(2)当a=0,b≠0时,得到一个一元一次方程,则直线l与圆锥曲线C相交,且只有一个交点,此时,若C为双曲线,则直线l与双曲线的渐近线的位置关系是平行；若C为抛物线,则直线l与抛物线的对称轴的位置关系是平行或重合.

2、直线与圆锥曲线的相交弦的弦长

3、中点弦的重要结论：

4、圆锥曲线的几个特殊结论：

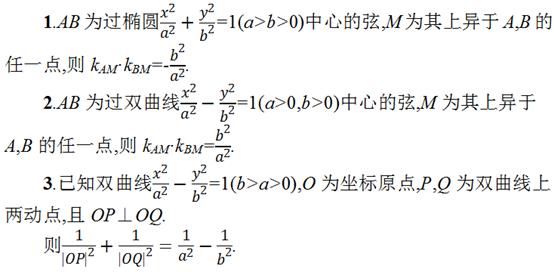
4.不垂直于x轴的直线与抛物线y^2=2px(p>0)交于不同的两点P,Q,点M(m,0)(m<0),则直线PQ过定点(-m,0)的充要条件是x轴是∠PMQ的角平分线.

5.直线l与抛物线y^2=2px(p>0)交于A(x1,y1),B(x2,y2)两点,则直线l与x轴交于M(m,0)的充要条件是y1y2=-2pm.特别地,直线l过焦点的充要条件是y1y2=-2p^2.

6.过点M(m,0)的直线l与抛物线y^2=2px(p>0)交于A(x1,y1),B(x2,y2)两点,则抛物线在A,B两点的切线交于点

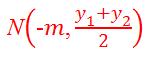
二、典题剖析

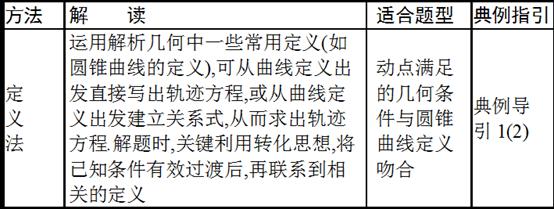
角度1、轨迹问题

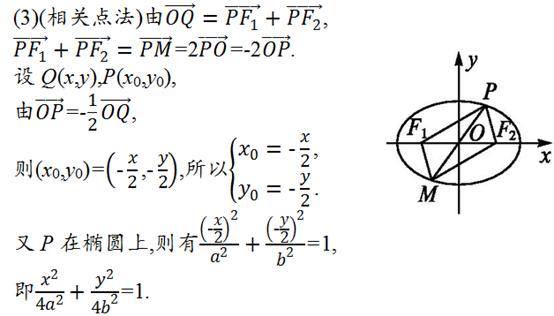
点评：

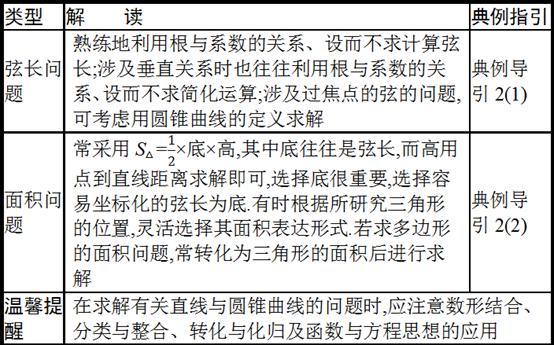
角度2、圆锥曲线弦长、面积问题

点评：

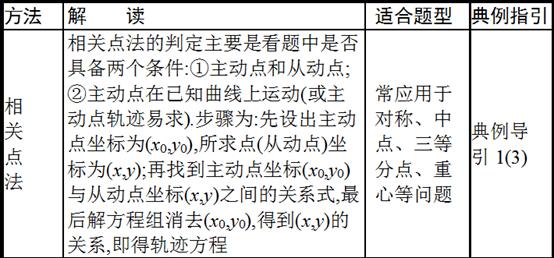
角度3、点差法问题

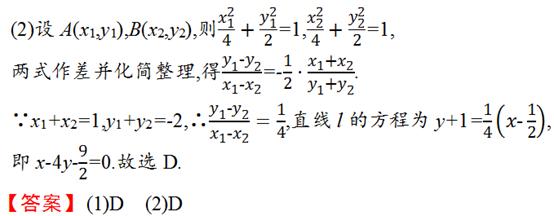
点评：

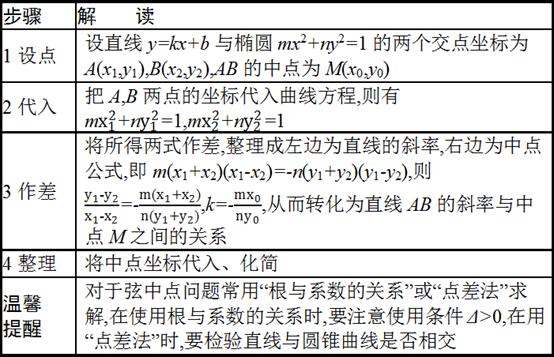
角度4、最值与范围问题

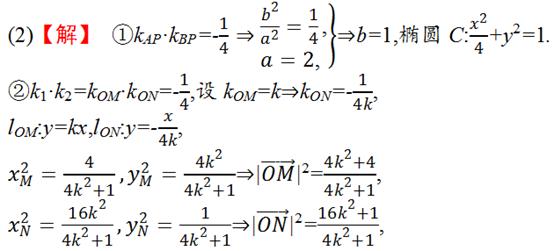
点评：

角度5、存在性问题

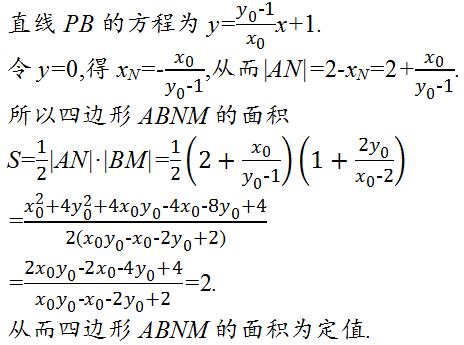
点评：

三、真题提升

圆锥曲线在高考中比重比较大，大家平常联系也少不了，我这里就举一个例子，重点对做题步骤以及得分要点做一个说明，希望对大家有所启发。

评分细则：

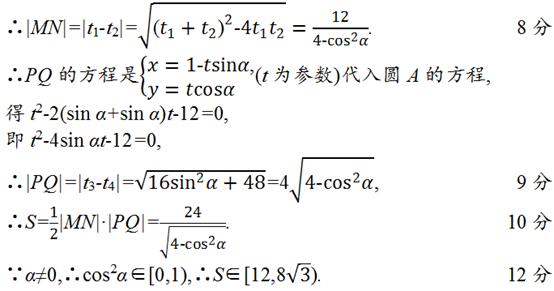
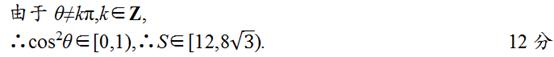
点评：

解答第二问中得分点

(1)求|MN|时,不写根与系数的关系,只要求对|MN|的给2分,但有些求|MN|时,没化简,只要经过简单化简对的,也给2分;

(2)求|PQ|时,不论用什么方法,只要求对给1分;

(3)S 的最简表达式对的给1分;

(4)只要有验证l⊥x 轴时,S=12的给1分.

解析几何解答题的阅卷原则

(1)当“合理”与“公平”矛盾时,选择公平,即用评分细则处理试卷,即使不太合理,为了公平,也得遵守.例如:解答题答案中只有一个正确结果,也要给一分.不管他是如何得到的.

(2)当证明过程较长时,可以引用大家熟知的结论不扣分.

(3)保持数学学科的特点,注重解题过程的严谨性.要求考生养成表达完整、推理严谨的良好习惯,注意答题的规范性,必不可少的步骤必须写出来,以减少扣分.

压轴解答题的答题技巧

(1)在解题的过程中,要把所需的条件和结论写全,中间的步骤可以省略,即中间环节的证明有误或空缺,可以跳过去往下演算,写出结论,这样后面部分仍可得分.因数学第一问与第二问独立计分,当第一问做不好时,别放弃,可以借用第一问要证的结论来解第二问,只是不给前一问的分而已.

(2)题目再难,每个题目中的条件总是可以推导出结论的,哪怕是只推导出一个结论,也可能是得分点,实在不行,写出题中应该用到的公式,也是有得分点的.