中考数学，专题复习：二次函数与圆相关的综合问题

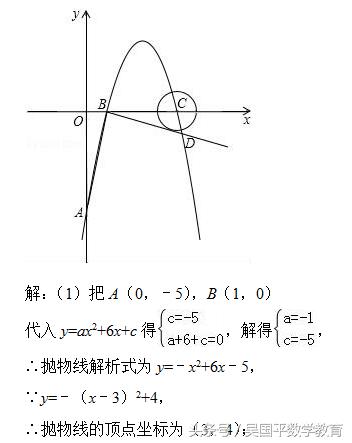
如图，在平面直角坐标系中，抛物线y=ax2+6x+c（a≠0）交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，﹣5），点B的坐标为（1，0）．

（1）求此抛物线的解析式及定点坐标；

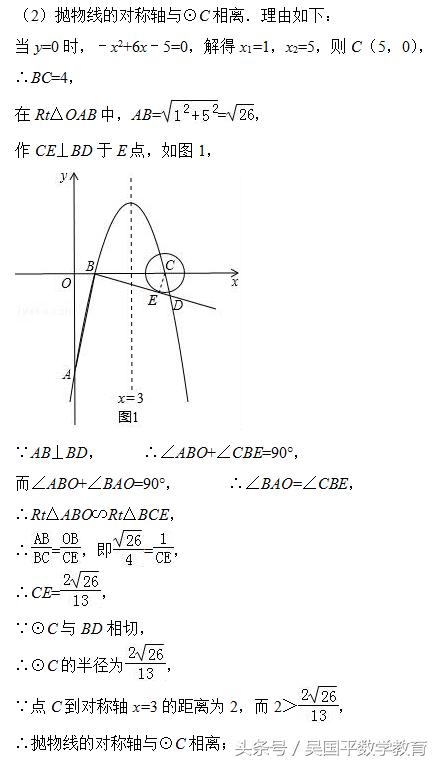
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并说明理由；

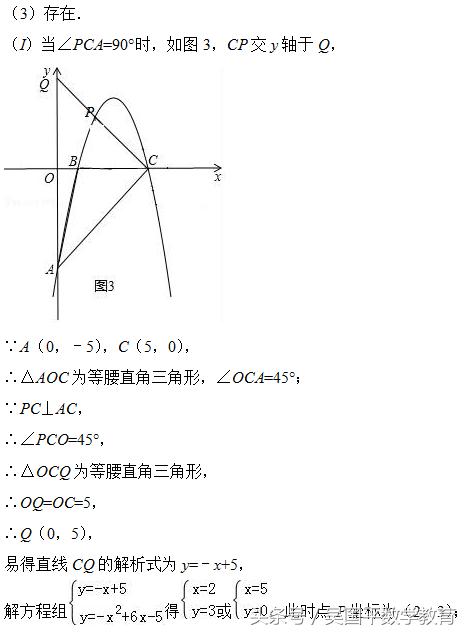
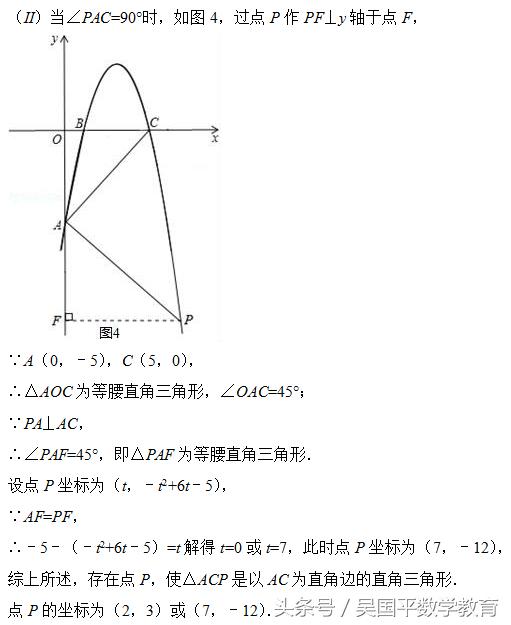
（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

考点分析：

二次函数综合题．

题干分析：

（1）把A（0，﹣5），B（1，0）代入y=ax2+6x+c得关于a、c的方程组，然后解方程组即可，再把解析式配成顶点式即可得到抛物线的顶点坐标；

（2）先解方程﹣x2+6x﹣5=0得C（5，0），则BC=4，再利用勾股定理计算出AB，作CE⊥BD于E点，如图1，证明Rt△ABO∽Rt△BCE，利用相似比可计算出CE，则根据切线的性质得到⊙C的半径，然后根据直线与圆的位置关系的判定方法判断抛物线的对称轴与⊙C的位置关系；

（3）讨论：当∠PCA=90°时，如图3，CP交y轴于Q，利用△AOC为等腰直角三角形可得到△OCQ为等腰直角三角形，则直线CQ的解析式为y=﹣x+5，于是通过解方程组得此时点P坐标；当∠PAC=90°时，如图4，过点P作PF⊥y轴于点F，利用△AOC为等腰直角三角形得到△PAF为等腰直角三角形．设点P坐标为（t，﹣t2+6t﹣5），则﹣5﹣（﹣t2+6t﹣5）=t，然后解方程求出t即可得到此时点P坐标．