洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。这种方法主要是在一定条件下通过分子分母分别求导再求极限来确定未定式的值。
函数与导数是高考命题中的重要内容,纵观最近几年的全国卷压轴题,几乎都是函数与导数的应用问题,其中求参数的取值范围又是重点考察的题型,针对此类问题,我们往往会引导学生运用分离变量的方法后,出现分式的形式,即数学分析中不定式的问题,处理这类问题有效方法就是运用洛必达法则。




















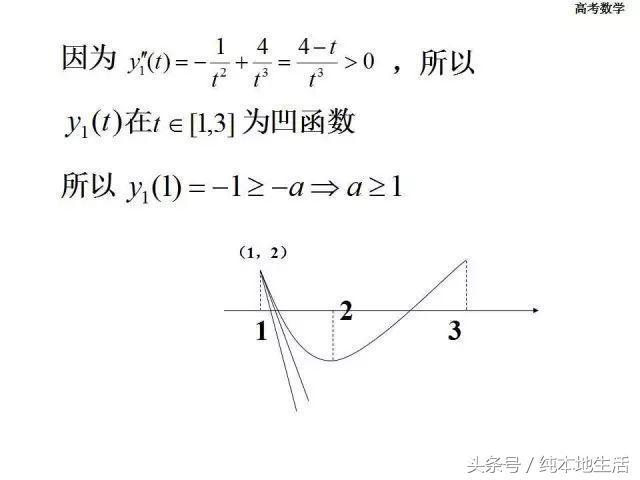

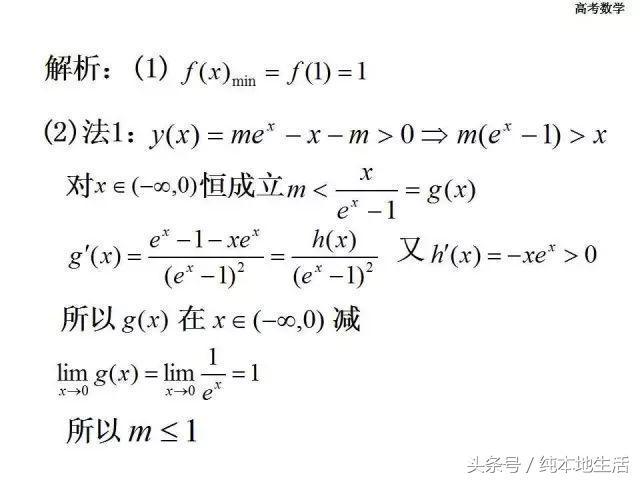
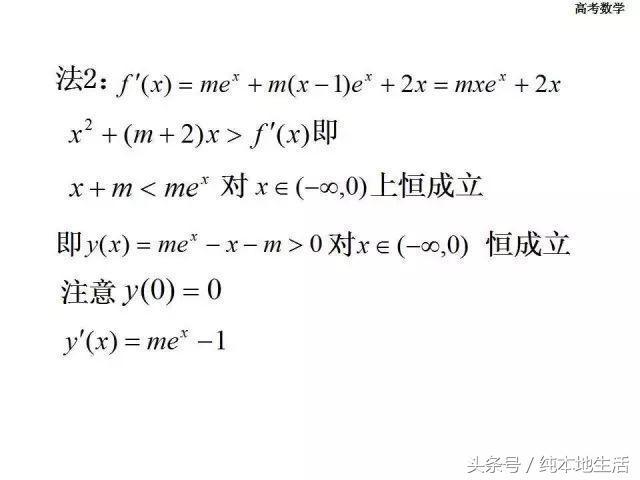




洛必达法则在解高考数学试题中的应用
洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。这种方法主要是在一定条件下通过分子分母分别求导再求极限来确定未定式的值。
函数与导数是高考命题中的重要内容,纵观最近几年的全国卷压轴题,几乎都是函数与导数的应用问题,其中求参数的取值范围又是重点考察的题型,针对此类问题,我们往往会引导学生运用分离变量的方法后,出现分式的形式,即数学分析中不定式的问题,处理这类问题有效方法就是运用洛必达法则。






















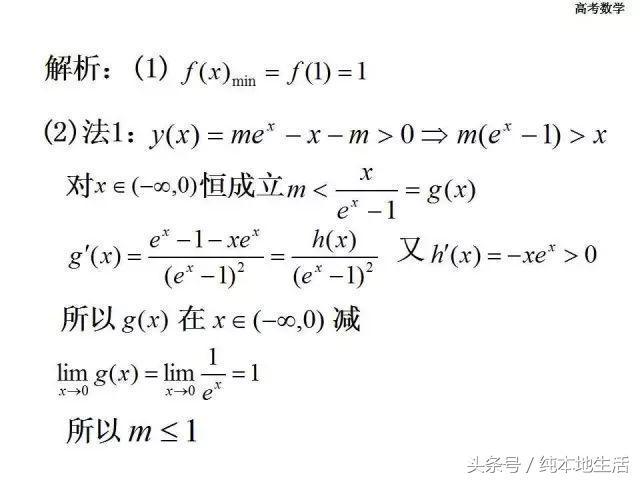




上一篇 : 高中数学:三角函数、立体几何强化专题总结
下一篇 : 曲线系的应用中常见错误及解决策略
高中7种常用函数图象及4种函数图象变换规则
高中数学必刷题大集合(含答案)
高考数学中外接球你必须掌握的秒杀技巧
 加载中,请稍侯......
加载中,请稍侯......
精彩评论