中考数学，专题复习：二次函数综合题

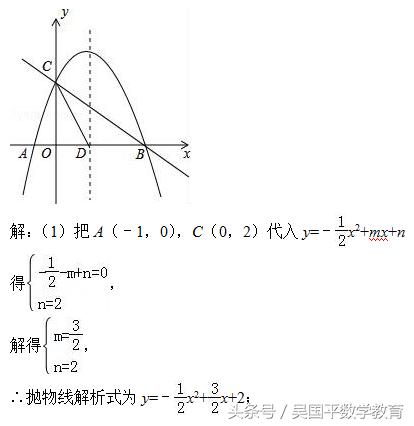
如图，抛物线y=﹣x2/2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．

（1）求抛物线的表达式；

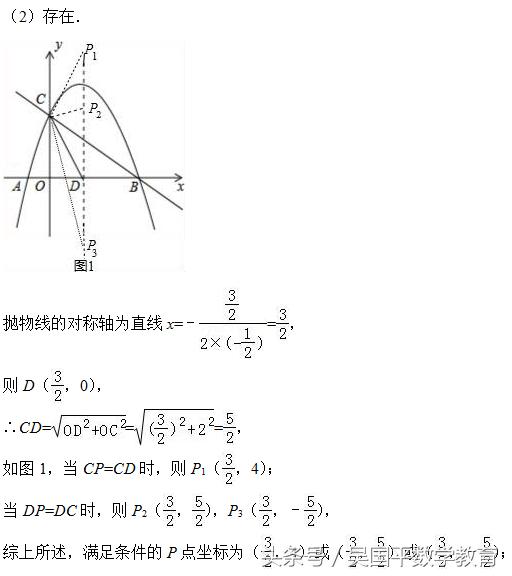
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；

（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

考点分析：

二次函数综合题．

题干分析：

（1）直接把A点和C点坐标代入y=﹣x2/2+mx+n得m、n的方程组，然后解方程组求出m、n即可得到抛物线解析式；

（2）先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣3/2，则D（3/2，0），则利用勾股定理计算出CD=5/2，然后分类讨论：如图1，当CP=CD时，利用等腰三角形的性质易得P1（3/2，4）；当DP=DC时，易得P2（3/2，5/2），P3（3/2，﹣5/2）；

（3）先根据抛物线与x轴的交点问题求出B（4，0），再利用待定系数法求出直线BC的解析式为y=﹣x/2+2，利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征，设E（x，﹣x/2+2）（0≤x≤4），则F（x，﹣x2/2+3x/2+2），则FE=﹣x2/2+2x，由于△BEF和△CEF共底边，高的和为4，则S△BCF=S△BEF+S△CEF=4•EF/2=﹣x2+4x，加上S△BCD=5/2，所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+5/2（0≤x≤4），然后根据二次函数的性质求四边形CDBF的面积最大，并得到此时E点坐标．