如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是．
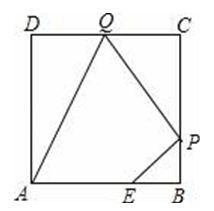
【考点】轴对称-最短路线问题；正方形的性质．
【分析】根据最短路径的求法，先确定点E关于BC的对称点E′，再确定点A关于DC的对称点A′，连接A′E′即可得出P，Q的位置；再根据相似得出相应的线段长从而可求得四边形AEPQ的面积．
上一篇 : 人教版七年级数学下册期中综合检测试卷
下一篇 : 初中数学：压轴题四边形综合题
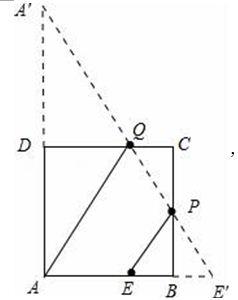
初中数学：轴对称+最短路线问题+正方形的性质结合
【考点】轴对称-最短路线问题；正方形的性质．
【分析】根据最短路径的求法，先确定点E关于BC的对称点E′，再确定点A关于DC的对称点A′，连接A′E′即可得出P，Q的位置；再根据相似得出相应的线段长从而可求得四边形AEPQ的面积．
上一篇 : 人教版七年级数学下册期中综合检测试卷
下一篇 : 初中数学：压轴题四边形综合题
初中数学，“将军饮马”的七大模型
人教版八年级数学上册第一章单元测试题（含答案）
初二《全等三角形》数学模型之“一线三等角”模型
加载中,请稍侯......
精彩评论