中考数学，专题复习48：解直角三角形的应用

典型例题分析1：

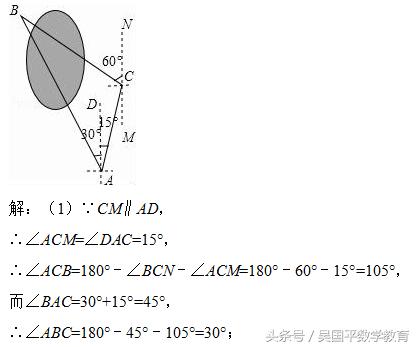
小明要测量公园被湖水隔开的两棵大树A和B之间的距离，他在A处测得大树B在A的北偏西30°方向，他从A处出发向北偏东15°方向走了200米到达C处，测得大树B在C的北偏西60°方向．

（1）求∠ABC的度数；

（2）求两棵大树A和B之间的距离（结果精确到1米）

考点分析：

解直角三角形的应用﹣方向角问题．

题干分析：

（1）先利用平行线的性质得∠ACM=∠DAC=15°，再利用平角的定义计算出∠ACB=105°，然后根据三角形内角和计算∠ABC的度数；

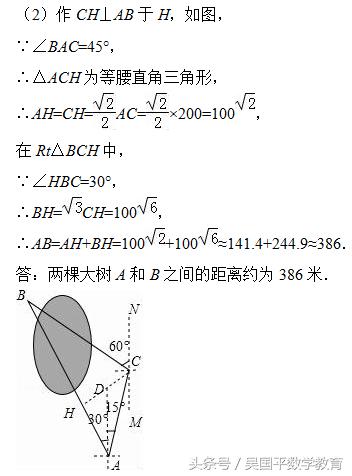
（2）作CH⊥AB于H，如图，易得△ACH为等腰直角三角形，则可以得到AH、CH、AC三者之间的关系，在Rt△BCH中利用含30度的直角三角形三边的关系得到BH、CH、AB、AH几者之间的关系，然后进行近似计算即可。

解题反思：

本题考查了解直角三角形的应用﹣方向角问题：在解决有关方向角的问题中，一般要根据题意理清图形中各角的关系，有时所给的方向角并不一定在直角三角形中，需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角．解决此题的关键作CH⊥AB构建含特殊角的直角三角形。

典型例题分析2：

如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．

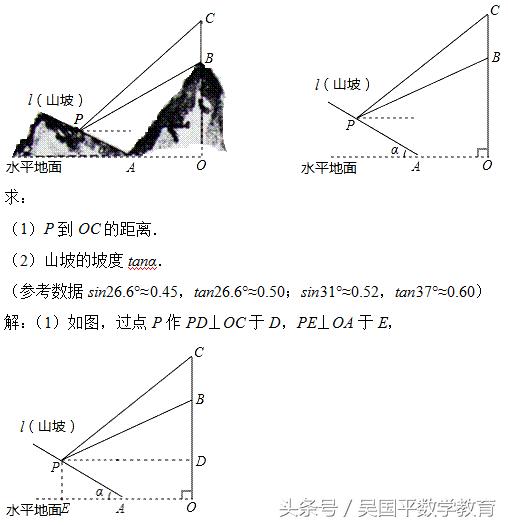
则四边形ODPE为矩形．

在Rt△PBD中，

∵∠BDP=90°，∠BPD=26.6°，

∴BD=PD•tan∠BPD=PD•tan26.6°；

在Rt△CPD中，

∵∠CDP=90°，∠CPD=31°，

∴CD=PD•tan∠CPD=PD•tan31°；

∵CD﹣BD=BC，

∴PD•tan31°﹣PD•tan26.6°=40，

∴0.60PD﹣0.50PD=40，

解得PD=400（米），

∴P到OC的距离为400米；

（2）在Rt△PBD中，BD=PD•tan26.6°≈400×0.50=200（米），

∵OB=240米，

∴PE=OD=OB﹣BD=40米，

∵OE=PD=400米，

∴AE=OE﹣OA=400﹣300=100（米），

∴tanα=PE/AE=40/100=0.4，

∴坡度为0.4．

考点分析：

解直角三角形的应用﹣仰角俯角问题；解直角三角形的应用﹣坡度坡角问题．

题干分析：

（1）过点P作PD⊥OC于D，PE⊥OA于E，则四边形ODPE为矩形，先解Rt△PBD，得出BD=PD•tan26.6°；解Rt△CPD，得出CD=PD•tan31°；再根据CD﹣BD=BC，列出方程，求出PD=400即可求得点P到OC的距离；

（2）利用求得的线段PD的长求出PE=40，AE=100，然后在△APE中利用三角函数的定义即可求解．

解题反思：

本题考查了解直角三角形的应用﹣仰角俯角问题、坡度坡角问题，难度适中，通过作辅助线，构造直角三角形，利用三角函数求解是解题的关键。