中考数学，专题复习45：二次函数综合题型

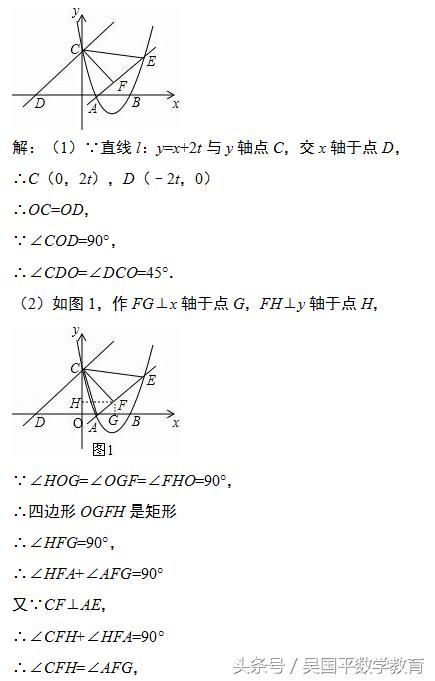
如图，已知抛物线经过点A（2，0）和B（t，0）（t≥2），与y轴交于点C，直线l：y=x+2t经过点C，交x轴于点D，直线AE交抛物线于点E，且有∠CAE=∠CDO，作CF⊥AE于点F．

（1）求∠CDO的度数；

（2）求出点F坐标的表达式（用含t的代数式表示）；

（3）当S△COD﹣S四边形COAF=7时，求抛物线解析式；

（4）当以B，C，O三点为顶点的三角形与△CEF相似时，请直接写出t的值．

考点分析：

二次函数综合题。

题干分析：

（1）求出点C，D的坐标，得到OC=OD，即可解答；

（2）如图1，作FG⊥x轴于点G，FH⊥y轴于点H，利用已知条件证明△FGA≌△FHC，得到FH=FG，HC=AG，设F（m，m）则2t﹣m=m﹣2，求出m的值，即可解答；

（3）如图2，作ET⊥HF于T，分别得到E的横坐标是（t2+1）/（t-1），CH=t﹣1，FT=2/（t-1），再由△HCF∽△TFE，得到CH/FT=CF/EF，即（t2+1）/（t-1）=CF/EF，分类讨论：当△OBC∽△FEC时；当△OBC∽△FCE时；求出t的值，即可解答。

解题反思：

本题考查了二次函数的性质、全等三角形的性质定理与判定定理、相似三角形的性质定理与判定定理，解决本题的关键是作出辅助线，构建全等三角形、相似三角形，并进行分类讨论。