中考数学压轴题，如何解函数与几何综合问题篇：二次函数与正方形

什么是正方形？

有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。

什么是二次函数？

一般地，如果y=ax2+bx+c（a,b,c是常数，a≠0），那么y叫做x 的二次函数。

y=ax2+bx+c（a,b,c是常数，a≠0）叫做二次函数的一般式。

正方形与二次函数作为初中数学最重要知识内容之一，一直是中考数学热点和重点。像二次函数的重要性，相信不要老师多说，它一直是中考数学必考的热点，超过90%以上的压轴题都和二次函数有关。

正方形作为一种特殊的平行四边形，不仅具有一般平行四边形所有性质，更具自身特殊的性质，如：

1、具有平行四边形、矩形、菱形的一切性质；

2、正方形的四个角都是直角，四条边都相等；

3、正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角；

4、正方形是轴对称图形，有4条对称轴；

5、正方形的一条对角线把正方形分成两个全等的等腰直角三角形，两条对角线把正方形分成四个全等的小等腰直角三角形；

6、正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。

因此，在中考数学中，若把二次函数和正方形放在一起，就可以“创造”出很多具有综合性强、创新型、解法灵活等鲜明特点的题型。

中考数学，二次函数与正方形相关题型，典型例题分析1：

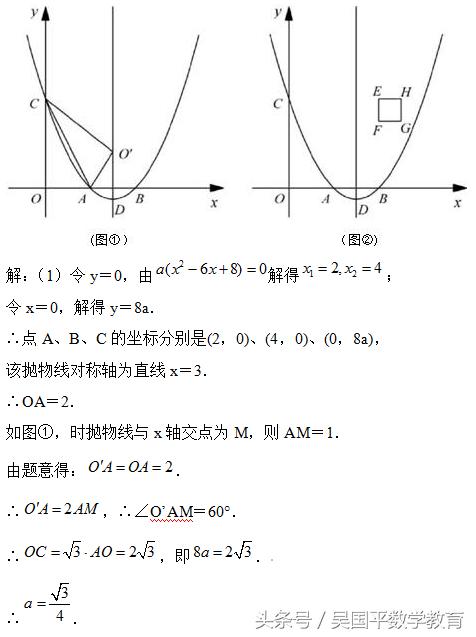
巳知二次函数y=a（x2-6x+8）（a＞0）的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．

（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的 对称轴上，求实数a的值；

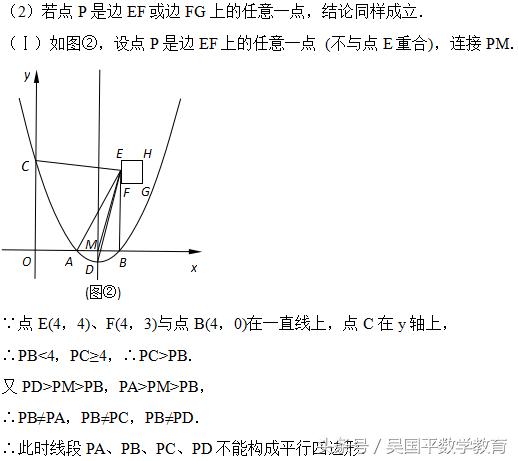
（2）如图②，在正方形EFGH中，点E、F的坐标分别是（4，4）、（4，3），边HG位于边EF的 右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等 （即这四条线段不能构成平行四边形）．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；

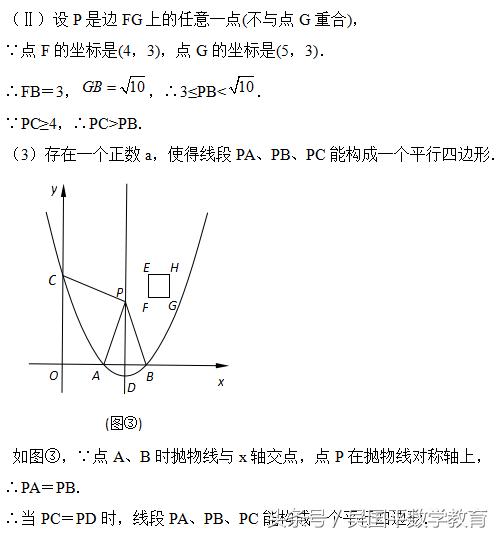
（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数阿a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等 （即这四条线段能构成平行四边形）？请说明理由．

考点分析：

二次函数综合题．

题干分析：

（1）本题需先求出抛物线与x轴交点坐标和对称轴，再根据∠OAC=60°得出AO，从而求出a．

（2）本题需先分两种情况进行讨论，当P是EF上任意一点时，可得PC＞PB，从而得出PB≠PA，PB≠PC，PB≠PD，即可求出线段PA、PB、PC、PD不能构成平行四边形．

（3）本题需先得出PA=PB，再由PC=PD，列出关于t与a的方程，从而得出a的值，即可求出答案．

解题反思：

本题主要考查了二次函数的综合问题，在解题时要注意运用数形结合和分类讨论，把二次函数的图象与性质和平行四边形的判定相结合是本题的关键．

二次函数与正方形相关题型本质上就是函数与几何综合类问题，此类问题一直是中考数学的热点。要想正确解决此类问题，除了要掌握好相应的几何知识和函数知识，更需要考生能根据图形的变化，找出变量之间的关系，从而建立起函数解析式。

函数与几何综合问题最大的特点就是“数”与“形”相互结合、相互渗透，二次函数与正方形相关的综合问题也不例外。

中考数学，二次函数与正方形相关题型，典型例题分析2：

如图所示，在平面直角坐标系xoy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B和D（4，-2/3）.

（1）求抛物线的表达式.

（2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动，同时点Q由点B出发，沿BC边以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动。设S=PQ2（cm2）.

①试求出S与运动时间t之间的函数关系式，并写出t的取值范围；

②当S取5/4时，在抛物线上是否存在点R，使得以点P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由.

（3）在抛物线的对称轴上求点M，使得M到D、A的距离之差最大，求出点M的坐标.

考点分析：

二次函数综合题；待定系数法求一次函数解析式；二次函数图象上点的坐标特征；待定系数法求二次函数解析式；勾股定理；平行四边形的性质.

题干分析：

（1）设抛物线的解析式是y=ax2+bx+c，求出A、B、D的坐标代入即可；（2）①由勾股定理即可求出，②假设存在点R，可构成以P、B、R、Q为顶点的平行四边形，求出P、Q的坐标，再分为三种情况：A、B、C即可根据平行四边形的性质求出R的坐标．（3）A关于抛物线的对称轴的对称点为B，过B、D的直线与抛物线的对称轴的交点为所求M，求出直线BD的解析式，把抛物线的对称轴x=1代入即可求出M的坐标。

解题反思：

本题主要考查了用待定系数法求一次函数和二次函数的解析式，勾股定理，平行四边形的性质，二次函数图象上点的坐标特征等知识点，解此题的关键是综合运用这些知识进行计算。此题综合性强，是一道难度较大的题目。