高考数学, 典型例题分析34：选择题讲解

高考数学选择题，典型例题讲解1：

设集合A={﹣1，0}，集合B={0，1，2}，则A∪B的子集个数是（　　）

A．4 B．8 C．16 D．32

解：集合A={﹣1，0}，集合B={0，1，2}，则A∪B={﹣1，0，1，2}，

∴集合A∪B的子集个数为24=16．

故选C．

考点分析：

并集及其运算；子集与真子集．

题干分析：

由集合A={﹣1，0}，集合B={0，1，2}，则A∪B={﹣1，0，1，2}，由此能求出集合A∪B的子集个数．

高考数学选择题，典型例题讲解2：

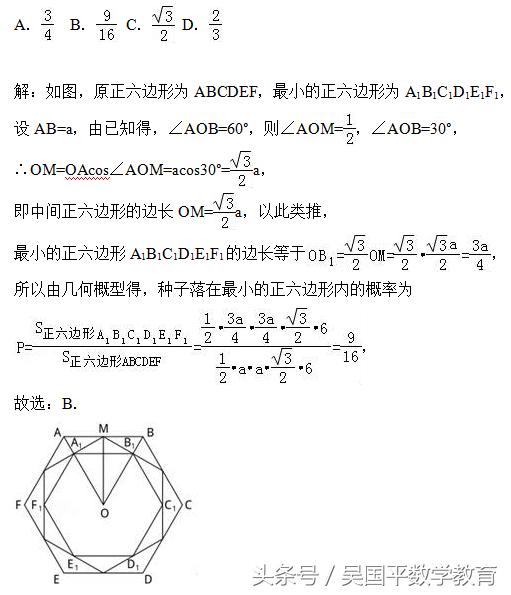
依次连接正六边形各边的中点，得到一个小正六边形，再依次连接这个小正六边形各边的中点，得到一个更小的正六边形，往原正六边形内随机洒一粒种子，则种子落在最小的正六边形内的概率为（　　）

考点分析：

几何概型．

题干分析：

求出最小的正六边形A1B1C1D1E1F1的边长，可得其面积，计算正六边形ABCDEF的面积，即可求出种子落在最小的正六边形内的概率．

高考数学选择题，典型例题讲解3：

函数f（x）=lnx﹣2/x的零点所在的大致区间是（　　）

A．（0，1） B．（1，2） C．（2，e） D．（3，4）

解：∵y=lnx为（0，+∞）上的增函数，y=﹣2/x在（0，+∞）上为增函数，

∴f（x）=lnx﹣2/x在（0，+∞）上为增函数，

又f（2）=ln2﹣1＜0，f（e）=lne﹣2/e=1﹣2/e＞0，

∴函数f（x）=lnx﹣2/x的零点所在的大致区间是（2，e）．

故选：C．

考点分析：

函数零点的判定定理．

题干分析：

由y=lnx为（0，+∞）上的增函数，y=-2/x在（0，+∞）上为增函数，可得f（x）=lnx﹣2/x在（0，+∞）上为增函数，再由f（2）＜0，f（e）＞0得答案．