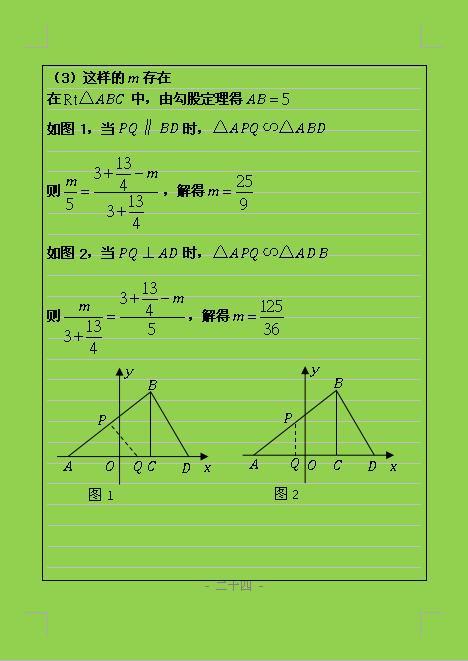
函数中因动点产生的相似三角形问题一般有三个解题途径:
① 求相似三角形的第三个顶点时，先要分析已知三角形的边和角的特点，进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式来表示各边的长度，之后利用相似来列方程求解。
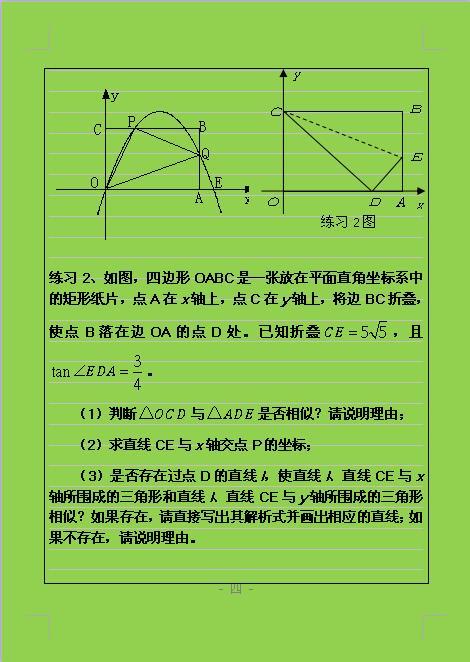
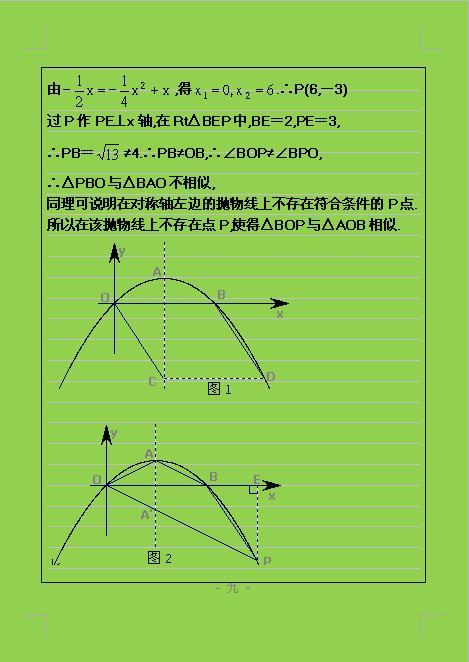
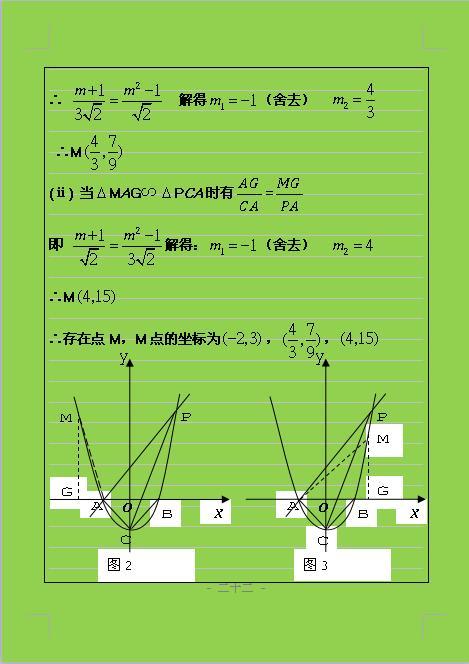
名校教师总结关于二次函数的动点问题，常用的解题途径有三种
名校教师总结关于二次函数的动点问题，常用的解题途径有三种
提示：键盘也能翻页，试试"← →"键
上一篇 : 八年级数学-三角形中位线1-基础加提高
下一篇 : 一元一次不等式组及其解法
加载中,请稍侯......
精彩评论