易错点

1. 二次函数的图象与系数a,b,c的符号的确定.

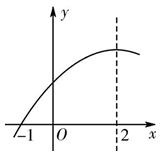
【例1】　二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:

① 4a+b=0;② 9a+c>3b;③ 8a+7b+2c>0;④ 当x>-1时,y的值随x值的增大而增大.

其中正确的结论有(　　).

A. 1个 B. 2个

C. 3个 D. 4个

难点分析

　根据抛物线的对称轴为直线X=-b/2a,则有4a+b=0;观察函数图象得到当x=-3时,函数值小于0,则9a-3b+c<0,即9a+c<3b;由于x=-1时,y=0,则a-b+c=0,易得c=-5a,所以8a+7b+2c=8a-28a-10a=-30a.再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小.

解答步骤

　∵　抛物线的对称轴为直线x=2,

∴　b=-4a,即4a+b=0,所以①正确.

∵　当x=-3时,y<0,

∴　9a-3b+c<0,即9a+c<3b.所以②错误.

∵　抛物线与x轴的一个交点为(-1,0),

∴　a-b+c=0.

而b=-4a,∴　a+4a+c=0,即c=-5a.

∴　8a+7b+2c=8a-28a-10a=-30a.

∵　抛物线开口向下,

∴　a<0.

∴　8a+7b+2c>0.所以③正确.

∵　对称轴为直线x=2,

∴　当-1<x<2时,y的值随x值的增大而增大,当x>2时,y随x的增大而减小.所以④错误.故选B.

误区纠错

本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;

一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);

抛物线与x轴交点个数由Δ决定,Δ=b2-4ac>0时,抛物线与x轴有2个交点;Δ=b2-4ac=0时,抛物线与x轴有1个交点;Δ=b2-4ac<0时,抛物线与x轴没有交点.

2. 二次函数和最值问题

【例2】　当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为(　　).

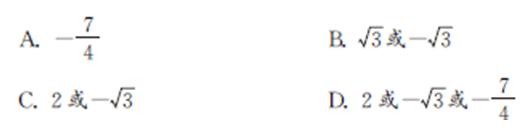
难点分析

　二次函数的最值得分类讨论问题,根据对称轴的位置,分三种情况讨论求解即可.

解答步骤

　二次函数的对称轴为直线x=m,

误区纠错

本题易错点在于不知分类讨论导致漏解.

要点掌握

1. 掌握二次函数的定义,能利用定义判断二次函数.

2. 能利用顶点式、交点式、三点式确定二次函数的解析式.

3. 会利用描点法画二次函数的图象并能说明其性质.

4. 能利用二次函数解析式中系数确定函数的对称轴、顶点坐标、开口方向与坐标轴的交点坐标等.