由于向量的线性运算和数量积运算具有先鲜明的几何背景，平面几何图形的许多性质，如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来，因此，可用向量方法解决平面几何中的一些问题。

定义法：

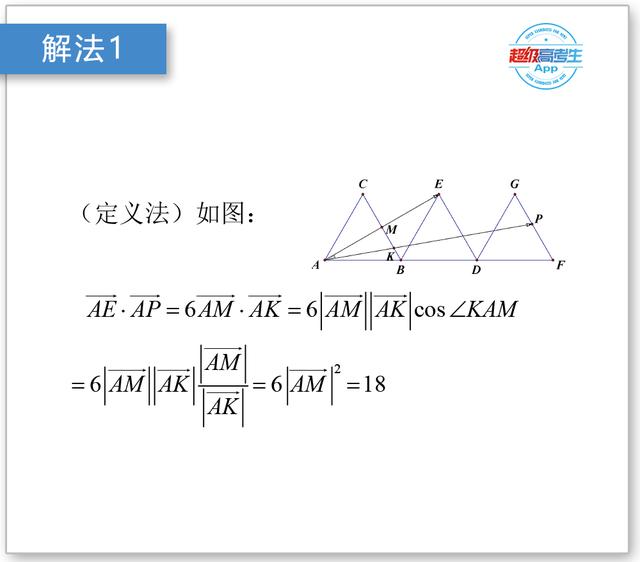
基底法：

坐标法：

特值法：

向量作为工具几何问题，开创了研究几何问题的新方法。向量的运算（运算律）与几何图形的性质有密切联系，向量的运算可以用图形简明地表示，而图形的一些性质又可以反映到向量的运算上来。

向量是近代数学中重要和基本的概念之一，有深刻的几何背景，是解决几何问题的有力工具，同时向量又是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景，在数学和物理学中都有广泛的应用。