小学数学应用题解题策略

1、一般应用题：

这类应用题没有固定的结构，也没有解题规律可循，完全要依赖分析题目中的数量关系找出解题的线索。

要点：从条件入手，要随时注意题目的问题；从问题入手，要随时注意题目的已知条件。

例题1、某加工厂要生产1100个零件，已经生产了5天，平均每天生产130个。如果剩下的平均每天生产150个，还 需要几天完成？

解题思路：

已知“已经生产了5天，平均每天生产130个”，就可以求出已经生产的个数。

已知“要生产1100个机器零件”和已经生产的个数，已知“剩下的平均每天生产150个”，就可以求出还需几天完成。

解答过程：

解： 【1100 - （130 × 5）】÷ 150 = 3 （天）

答：剩下的还需 3 天完成。

2、 典型应用题：

这类应用题一般需要用两步或两步以上的运算解答，有的题目由于具有特殊的结构，因而可以用特定的步骤和方法来解答，这样的应用题通常称为典型应用题。

例题2、（工程问题）一件工程，甲工程队修建需要8天，乙工程队修建需要12天，两队合修4天后，剩下的任务，有乙工程队单独修，还需几天？

要点：工程问题是研究工作效率、工作时间和工作总量的问题。

工作总量没有给出实际数量，把它看做“1”，工作效率用来表示，所求问题大多是合作时间。

解题思路：

把一件工程的工作量看作“1”，则甲的工作效率是1/8，乙的工作效率是1/12。

已知两队合修了4天，就可求出合修的工作量，进而也就能求出剩下的工作量。

用剩下的工作量除以乙的工作效率，就是还需要几天完成。　

解答过程：

解：　甲乙合修的工作量：（1/8 + 1/12）× 4 = 5/6 ,

剩下的乙单独修需要： （1- 5/6） ÷ 1/12 = 2 （天）。

答： 剩下的乙单独修需要 2 天 。

例题3、（归一问题）6台拖拉机4小时耕地300亩，照这样计数，8台拖拉机7小时可耕地多少亩？

要点：

题目的前部分是已知条件，是一组相关联的量；

题目的后半部分是问题，也是一组相关联的量，其中有一个量是未知的。

解题思路：

先求出单一的量，然后再根据问题，或求单一量的几倍是多少，或求有几个单一量。

先求出单一量，即1台拖拉机1小时耕地的亩数，再求8台拖拉机7小时耕地的亩数。

解答过程：

解：1台拖拉机1小时耕地的亩数： 300 ÷ 6 ÷ 4 = 12.5 （亩），

8台拖拉机7小时耕地的亩数： 12.5 × 8 × 7 = 700 （亩）。

答：8台拖拉机7小时耕地 700 亩。

例题4、（相遇问题）一列货车和一列客车同时从相距648千米的两地相对开出，4.5小时相遇。

客车每小时行80千米，货车每小时行多少千米？

要点：指两运动物体从两地以不同的速度作相向运动。

⑴相遇时间=相隔距离（两个物体运动时）÷速度和；

⑵ 相隔距离（两物体运动时）=速度之和×相遇时间；

⑶甲速=相隔距离（两个物体运动时）÷相遇时间－乙速。

解答过程：

解：648 ÷ 4.5 - 80 = 64 （千米/小时）

答：货车每小时行驶 64 千米。

注意：相遇问题可以有不少变化。如两个物体从两地相向而行，但不同时出发；或者其中一个物体中途停顿了一下；或两个运动的物体相遇后又各自继续走了一段距离等，都要结合具体情况进行分析。

3、特殊应用题：

对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题：

例题5、有两个自然数A和B，如果把A增加12，B不变，积就增加72；如果A不变，B增加12，积就增加12O，求原来两数的积。

要点：借助画平面图帮助思考解题。

解题思路：

根据题目的条件比较抽象的特点，不妨借用长方形图，把条件转化为因数与积的关系。

先画一个长方形，长表示A，宽表示B，这个长方形的面积就是原来两数的积。如图（l）所示。

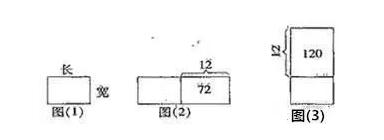
图a

根据条件把A增加12，则长延长12，B不变即宽不变，如图（2）；

同样A不变即长不变，B增加12，则宽延长12，如图（3）。

从图中不难找出：

原长方形的长（A）是120÷12＝10；

原长方形的宽（B）是72÷12＝6；

则两数的积为1O×6＝6O。

借助长方形图，弄清了题中的条件，找到了解题的关键。

例题6、用3个长3厘米、宽2厘米、高1厘米的长方体，拼成一个大长方体。这个大长方体的表面积是多少？

要点：一些求积题，结合题目的内容画出立体图，这样做，使题目的内容直观、形象，有利于思考解题。

解题思路：

按题意画立体图来表示，三个长方体拼成的大长方体有以下三种情况：

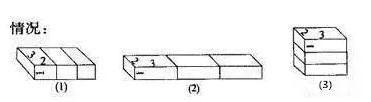
图b

（l）拼成长方体的长是2×3＝6（厘米），宽3厘米，高1厘米。表面积为（6×3＋6×l＋3×l）×2＝54（平方厘米）。

（2）拼成长方体的长是3×3＝9（厘米），宽2厘米，高1厘米。表面积为（9×2＋9×1＋2×1）×2＝58（平方厘米）。

（3）拼成长方体的长是3厘米，宽是2厘米，高是1×3＝3（厘米）。表面积为（3×2＋3×3＋2×3）×2＝42（平方厘米）。

这道题有以上三种答案，通过画图起到审题和理解题意的作用。

例题7、甲乙两人同时从相距88千米的两地相向而行，8小时后在距中点4千米处相遇。甲比乙速度快，甲、乙每小时各行多少千米？

要点：题目条件多，条件之间关系复杂，一时难以解答，可画线段图表示，寻求解题的突破口。

解题思路：

按照题意画线段图：

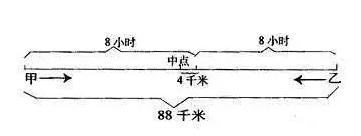
图c

从图中可以清楚看出，甲、乙8小时各行的距离，甲行全程的一半又多出 4千米，乙行全程的一半少 4千米，这样就可以求出甲、乙的速度了。

甲速：（88÷2＋4）÷8＝6（千米）

乙速：（88÷2－4）÷8＝5（千米）

总结：解题时通过画图来帮助理解题意，起到了化繁为简、化难为易的作用，我们在解题中要广泛使用。