高频核心考点

一、垂径定理

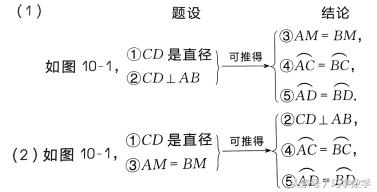
（1）垂径定理及相关命题如下表所示：

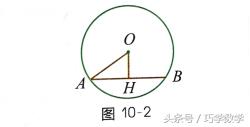
（4）“金三角”模型，如图10 -2，由OH，AH,AO组成的直角三角形，可用勾股定理进行计算.

二、圆周角定理

在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

推论1: 在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等，

推论2: 半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径。

三、切线的性质和判定

1、切线的判定

2、切线的性质

后三者中有两条成立，则另一条也成立。

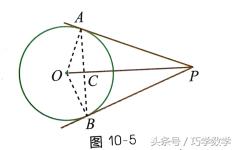
四、切线长定理

五、弦切角及定理

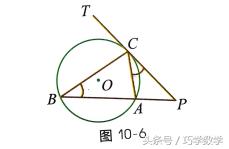
1、顶点在圆上，一边和圆相交，另一边和圆相切的角叫作弦切角(弦切角就是切线与弦所夹的角).如图10-6,直线PT切圆O于点C,BC,AC 为圆O的弦，∠TCB,∠TCA,∠PCA,∠PCB都是弦切角.

(2 )弦切角定理: 弦切角的度数等于它所夹的弧的度数的一半.

推论: 弦切角等于它所夹的弧所对的圆周角.如图10-6,可知∠TCB=∠CAB.

方法技巧提炼

圆中常见的辅助线的作法，通常可以考虑:

1.作半径.

(1)连半径、造等腰;

(2)作过切点的半径;

(3)作半径和弦心距.

2.作直径或直径所对的圆周角构造直角三角形.

3.切线的证明.

(1)已知是交点: 连半径，证垂直; (2 )不知是交点: 作垂直，证半径.

4.遇弦长可构造垂径定理模型.

5.两圆相切可作两圆公切线或连心线.

6.两圆相交可作两圆公共弦.

7.出现圆心角可以考虑构造弦所对的圆周角，反之亦可.