一、特值法的含义

遇到复杂问题时，通过设题干中的某些未知量为特殊值，从而达到方便计算快速得到结果的方法。

这个神奇的方法可以用来解决哪些题目呢?接下来我们就一起学习特值法的常见应用。

二、特值法的常见应用

1.几何问题

如图，平行四边形ABCD的面积是54平方米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上任意一点，则阴影部分的面积为( )平方厘米。

数量关系考试：利用特值法巧解数学运算

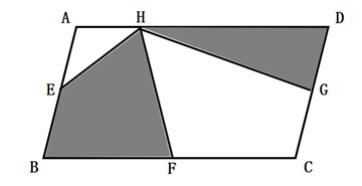
解析：因为H为AD边上任意一点，而答案又是定值，所以与H点的位置无关。(1)设H点与A点重合，阴影部分变ΔABF和ΔADG，由于ΔABF和ΔACF是等底等高，所以ΔABF和ΔACF面积相等，同理ΔAGC和ΔADG面积相等，故阴影部分面积为平行四边形ABCD的面积的一半，即27平方厘米。(2)设H点为AD边的中点，ΔAEH=ΔHDG=1/2ΔHEG，同理ΔEBF=ΔGCF=1/2ΔEFG，所以阴影部分面积为平行四边形ABCD的面积的一半，即27平方厘米。

总结：当几何问题中出现任意一点时，把任意点设为端点或中点。

2.计算类问题

数量关系考试：利用特值法巧解数学运算

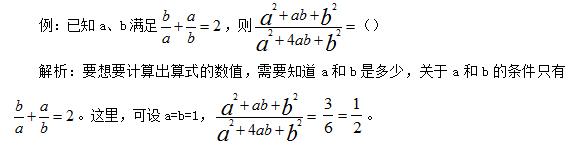
总结：简单计算类问题，把未知量设成简单计算的数。

3.利润问题

例：某商品2月份价格较1月份上涨了20%，由于政府调控政策的出台，3月份该商品又降了20%，问该商品3月份的价格与1月份的价格相比( )。

A.涨高了 B.持平 C.降低了 D.不能确定

解析：想要求出3月份的价格与1月份相比是涨高还是降低了，需要知道3月份和1月份的价格分别是多少。从题目信息出发，只给出上涨和下降的幅度，我们可设最开始的月份1月份的价格为100，那么2月份的价格就为100×(1+20%)=120，3月份的价格为120×(1-20%)=96，3月份的价格<1月份的价格，所以是降低了，选择C。

总结：在利润问题中，经常把成本或者售价设为10或100。