指数函数、对数函数是高一数学中初等函数中的两个典型函数。运用指对函数图像和性质解决问题，是很常见的题型。这就需要同学们对指对函数图像变换非常熟悉。今天我们举一个例题，来说明一下如何使用数形结合思想解决指对方程相关问题。

题例：

题目

分析：

这是一个方程，我们要向使用数形结合思想解决问题，就要构造函数。这个方法，在函数与方程思想里是个很基础的方法。有时候，需要对方程进行同解变形，然后再确定两个函数，目的是使构造出来的函数更接近课本所讲的基本初等函数，或者找到一条直线以简化函数关系。

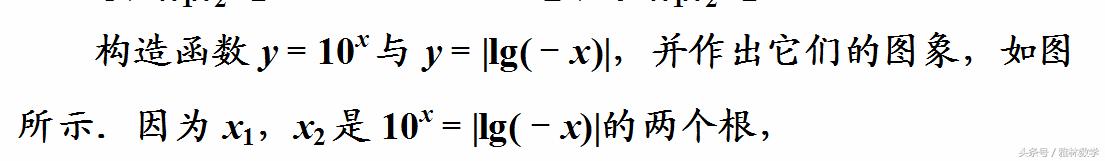
根据方程构造出两个函数，并说明问题如何转化

作图：

把构造出来的函数图像在同一个坐标系内做出来。这样，方程的解就是两个函数图像交点的横坐标，方程的解的问题，就转化为函数图像和性质问题。

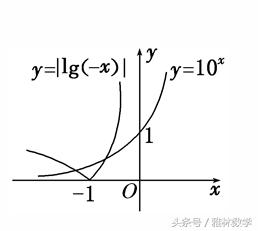
两个交点的横坐标就是方程的两个解

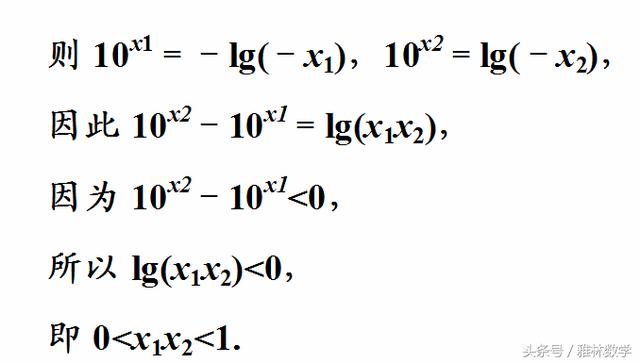
利用函数图像和性质特征进行分析

选出答案

你学会了吗？