相似三角形这部分知识难度较大,与全等三角形有本质的差异,判定全等三角形是直观上就能判断出哪两个三角形全等,利用全等三角形的判定定理来证明即可,相似三角形的判定难在学生看不出来哪两个三角形相似,即使将相似三角形的判定定理全部背诵下来,也有无的放矢之嫌;这就需要平时积累经验,找出规律即技巧。我在这篇文章中将相似这部分知识做详细梳理。
一.相似
相似图形:形状相同的图形。
相似多边形:对应边成比例,对应角相等的两个多边形。
相似多边形的性质:相似多边形的对应角相等,对应边的比相等。
相似比:相似多边形对应边的比称为相似比。
网络图片
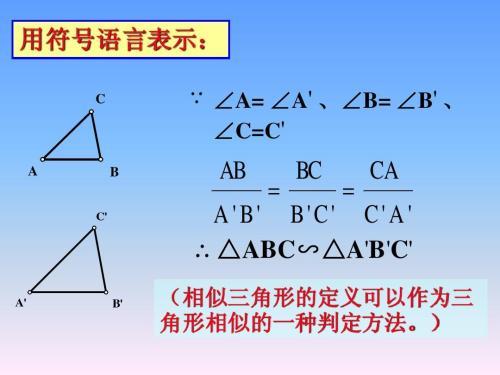
二.相似三角形:是形状相同的三角形,它们的对应角都相等,对应边的比都相等,对应边的比称为相似比。
三.相似三角形的判定定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
如果两个三角形的两组对应边的比相等,相应的夹角对应相等,那么这两个三角形相似。
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
四.相似三角形的定义是相似三角形的判定方法:如果两个三角形的对应角都相等,对应边的比都相等,那么这两个三角形相似。相似三角形的四个判定定理也是相似三角形的判定方法。
五.三角形内角平分线的性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例。
六.相似三角形的性质:
如果两个三角形相似,则它们的对应高的比、对应角平分线的比、对应中线的比、对应周长的比对应相似比。
相似三角形的面积比等于相似比的平分。
七.几种特殊的相似三角形
共边三角形:有一条公共边的两个三角形。
共角三角形:有一个角相等或互补的两个三角形。
共边共角三角形:有一个公共角而且有一条公共边的两个三角形。
八.位似图形:两个多边形不仅相似而且对应顶点的连线相交于一点,这样的两个图形叫做位似图形,这个点叫做位似中心。
九.解题技巧:构造相似形的方法是作平行线。
十.常见经典题型:
(一)巧解连比问题
例1.已知(x/3)=(x/4)=(z/5),求(x+y+z)/(x+y-z)的值。
解:设(x/3)=(x/4)=(z/5)=k,则x=3k y=4k z=5k (k≠0)
∴(x+y+z)/(x+y-z)=(3k+4k+5k)/(3k+4k-5k)=6
(二)用平行证明线段成比例
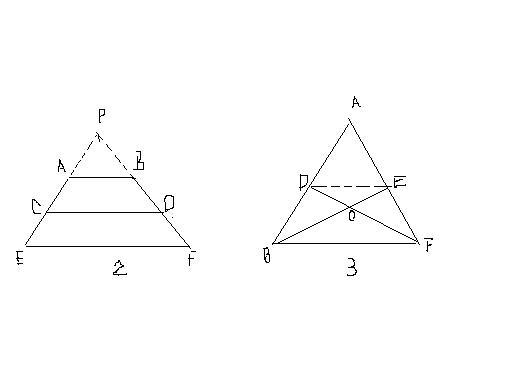
例2.AB∥CD∥EF,求证:AC/CE=BD/DF 如下图2
证明:延长EA、FB相交于点P
∵AB∥CD
∴△PAB∽△PCD
∴PA/PC=PB/PD
∴PA/(PA+AC)=PB/(PB+BD)→(PA+AC)/PA=(PB+BD)/PB→(1+AC/PA)=(1+BD/PB)→AC/PA=BD/PB→PB/PA=BD/AC
∵.AB∥EF
∴AE/PA=BF/PB→PB/PA=BF/AE
∴BD/AC=BF/AE→BD/BF=AC/AE
∴AC/(AC+CE)=BD/(BD+DF)
∴CE/AC=DF/BD,即AC/CE=BD/DF
自己手绘
(三)添加平行线,构造相似形
例3.在△ABC中,如上图3,D、E分别是AB、AC边的中点,且CD与BE相交于O点,求证:OC×OE=OD×OB 证明:连接DE,在△ABC中
∵D、E分别为AB、AC边的中点
∴DE∥BC
∴△ODE∽△OBC
∴OD/OC=OE/OB
∴OC×OE=OD×OB
还有用a/c=d/b代替ab=cd、用平行判定相似、相似三角形的实际应用题型,在做练习题巩固知识的同时,应该用心琢磨。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论