关于圆这部分知识在中考试卷中所占的比例很大，经常同二次函数、一元二次方程等知识结合在一起，所占的分值较大，因此要想中考数学获得高分，必须将圆这部分知识学懂弄通。

一.圆是中心对称图形

圆是以圆心为对称中心的中心对称图形，圆绕圆心旋转任何角度都能够与原来的图形重合，这种性质叫做圆的旋转不变性（圆特有的性质）。

二：圆心角：顶点在圆心的角。

特征：顶点在圆心，两边与圆相交，一般指小于平角的角，它所对的弧是劣弧。

三.圆心角、弧、弦之间的关系

定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

推论1：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等。

推论2：在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等。

注意：定理及推论可同一成：在同圆或等圆中，两条圆心角、两条弧、两条弦、两条弦心距，若有一组量相等，那么它们所对应的其余各组量也相等。

例1.⊙O的弦AB与半径OE、OF分别交于C、D，AC=BD，求证：⑴ OC=OD，⑵ AE弧=BF弧

关于中考重点内容圆的知识点系统梳理续篇


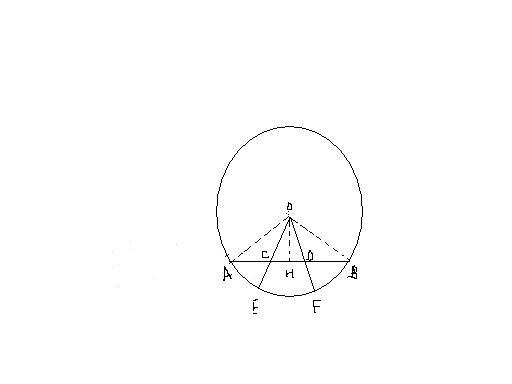
证明⑴：过O作OH⊥AB，垂足为H，则AH=BH.

∵AC=BD

∴CH=DH

∴OH是CD的垂直平分线

∴OC=OD

⑵ 连接OA、OB，则OA=OB

∵OH⊥AB

∴∠AOH=∠BOH（等腰三角形的“三线合一”性质）

同理∠COH=∠DOH

∴∠AOE=∠BOF

∴AE弧=BF弧

四.圆周角：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

特征：顶点在圆上，角的两边都与圆相交

五.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

注意：在同圆或等圆中，同弧或等弧所对的圆周角相等，是在圆中找相等角的方法。

六.圆周角定理和推论

推论1：半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。

推论2：在同圆或等圆中，相等的圆周角所对的弧也相等。

七.圆外角与它所夹的两段弧的关系：圆外角的度数等于它所夹的两段弧的度数差的一半。

关于中考重点内容圆的知识点系统梳理续篇


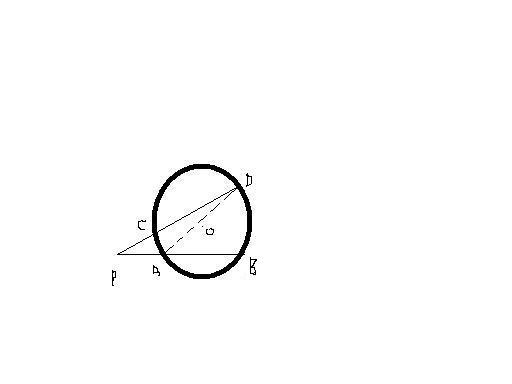
证明：连接AD

∵∠DAB的度数=BD弧度数的一半

∠ADP的度数=AC弧度数的一半

∴∠P=∠DAB－∠ADP=（BD弧度数－AC弧度数）的一半

圆外角：顶点在圆外，并且两边都和圆相交的角。

八.解题规律：

  1. 过圆心作弦的垂线段，是已知弦长求半径常见的辅助线作法。

  2. 证明弧相等，常常需证明它们所对应的另一组量相等，即圆心角相等或弦相等。

  3. 圆心角的度数等于它所对应的弧的度数。

  4. 有了直径，构造直角。