圆在几何中的地位举足轻重,中考试卷中经常和其他知识结合以压轴题的形式出现,因此,学好圆的知识是冲刺中考的前提和基础,我在这里将圆这部分知识以及重点题型做全面系统梳理。
一.圆的定义
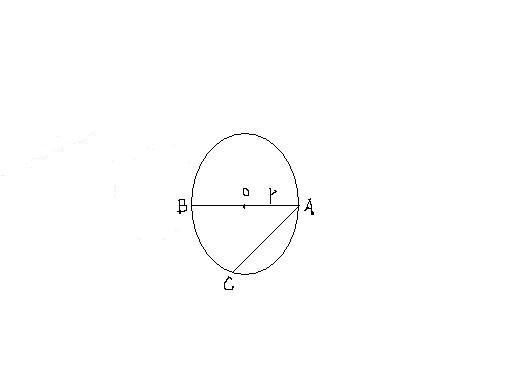
1.圆的描述性定义:在一个平面内,线段OA绕着它固定的一个端点O旋转一周,另一个端点A所形成的圆形叫做圆。固定的端点O叫做圆心,OA线段叫做半径,以点O为圆心的圆叫做⊙O
2.圆的集合性定义:圆心为O,半径为r的圆可以看做所有到定点O的距离等于定长r的点组成的图形。
自己手绘
3.解题方法:确定一个圆的两个要素是圆心和半径,其中圆心确定圆的位置,半径确定圆的大小。
4.弦:连接圆上任意两点的线段。如AB、AC
5.直径:经过圆心的弦。如AB
6.弧:圆上任意两点之间的部分叫做圆弧,简称弧.如AC弧
7.半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。大于半圆的弧叫做优弧;小于半圆的弧叫做劣弧。
注意:弧与弦是有区别的,弧是曲线,弦是线段;直径是圆中最长的弦,而弦不都是直径。如:AB是直径、也是弦,而AC是先、不是直径。
例题1.判断下列句子的对错:
①等于半径两倍的线段是直径。
解:这句话有错误,必须是圆的弦时为前提,等于半径两倍的线段才是直径。
②半圆是弧,弧是半圆。
解:这句话有错误,半圆是圆中的特殊弧;应改成半圆是弧,弧不一定是半圆。
③以P为圆心,以半径为r的圆有无数个。
解:这句话有错误,以P为圆心,以半径为r的圆只有一个。
二.垂直于弦的直径
1.圆的轴对称性:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。
注意:因为对称轴是一条直线,因此不能说任何一条直线是对称轴,圆有无数条对称轴,
画对称轴的技巧:过圆心的直线。
2.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
注意:①定理中的证明是利用圆的轴对称的性质证明的。
②定理中的直径应理解为过圆心的直线(或线段)。
③等弧是指在同圆或等圆中,能够互相重合的弧。
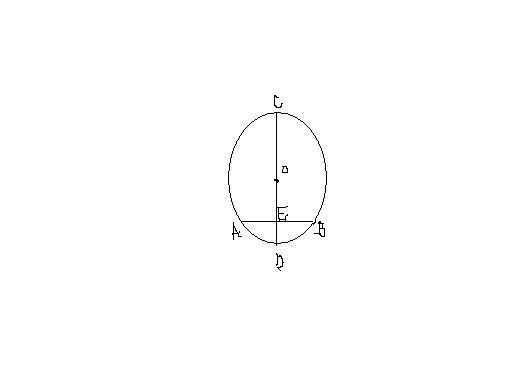
3.垂径定理的推论:
推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
推论3:平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
自己手绘图片
注意:⑴推论中平分的弦不能是直径,因为两条直径总是互相平分的,但不一定互相垂直。
⑵垂径定理及推论可以理解为垂径定理的条件和结论可分为五个事项:①CD是直径(过圆心O) ②CD垂直AB ③AE=BE ④ AD弧等于BD弧 ⑤ AC弧等于BC弧.
若其中两个事项成立,则其余三个事项也成立。
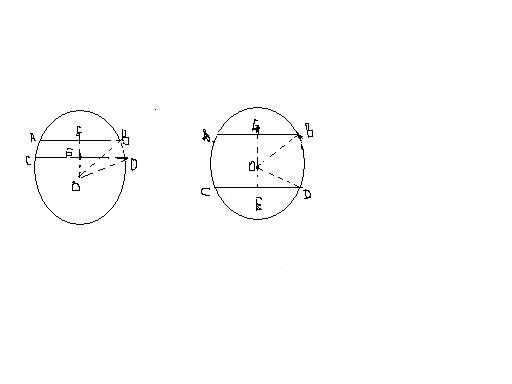
例2.⊙O的直径为50㎝,弦AB∥CD,且AB=40㎝,CD=48㎝,求弦AB和弦CD之间的距离。
自己手绘图片
解:当弦AB与CD在圆心的同侧时,如左图
作OG⊥AB于G,交CD与E,连接OB、OD
∵AB∥CD
∴OE⊥CD
∴EG为AB、CD之间的距离
∴BG=1/2 AB=1/2×40=20㎝
DE=1/2 CD=1/2×48=24㎝
在直角三角形DEO中,OE²=OD²-DE²=25²-24²=49,即OE=7㎝
在直角三角形BGO中,OG²=OB²-BG²=25²-20²=225,即OG=15㎝
∴EG=OG-OE=15-7=8㎝
解:当弦AB与CD在圆心的异侧时,如右图
作OG⊥AB于G,延长GO交CD与E,连接OB、OD
∵AB∥CD
∴OE⊥CD
∴EG为AB、CD之间的距离
∴BG=1/2 AB=1/2×40=20㎝
DE=1/2 CD=1/2×48=24㎝
在直角三角形DEO中,OE²=OD²-DE²=25²-24²=49,即OE=7㎝
在直角三角形BGO中,OG²=OB²-BG²=25²-20²=225,即OG=15㎝
∴EG=OG+OE=15+7=22㎝
综上所述,弦AB和CD之间的距离为22㎝和8㎝.
解题技巧:
①作半径构成三角形,把圆中的问题转化为三角形三边关系问题。
②作圆的半径,是圆的几何题在成见的辅助线作法。
③通过作弦心距(过圆心作弦的垂线段)构造三角形,是圆的几何题在成见的辅助线作法。
④ 在解决有关弦的问题时,常作垂直于弦的直径(过圆心作垂线段),应用垂径定理求解。
⑤ 连接圆心与中点,证明垂直,是圆的几何题在成见的辅助线作法。根据垂径定理的推论求解。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论