高考数学压轴百日冲刺快速提分秘籍 不等式的证明技巧

【高考地位】

证明数列不等式，因其思维跨度大、构造性强，需要有较高的证明技巧。这类问题的求解策略往往是：通过多角度观察所给数列通项的结构，深入剖析其特征，抓住其规律进行恰当地选择不等式的证明技巧. 在高考中常常以解答题出现，其试题难度属中高档题.

【方法点评】

方法一 比较法

使用情景：一般不等式证明

解题模板：第一步 通过两个实数a与b的差或商的符号（范围）确定a与b大小关系；

第二步 得出结论.

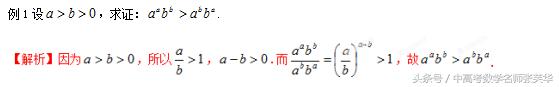
考点：不等式的证明.

方法二 分析法

使用情景：一般不等式证明

解题模板：第一步 从求证的不等式出发，分析这个不等式成立的充分条件；

第二步 把证明这个不等式的问题转化为证明这些条件是否具备的问题；

第三步 如果能够肯定这些条件都已具备，那么就可以判定所证的不等式成立.

考点：绝对值不等式的证明.

方法三 综合法

使用情景：一般不等式证明

解题模板：第一步 从已知或证明过的不等式出发，逐步推出其必要条件；

第二步 根据不等式的性质及公理推导出欲证的不等式；

第三步 得出结论.

考点：基本不等式证明不等式

方法四 放缩法

使用情景：一般不等式证明

解题模板：第一步 根据已知找出其通项公式an=f(n)；

第二步 然后运用恰当的放缩法对通项进行放缩；

第三步 利用数列求和公式即可得出结论.

考点：不等式的证明.

方法五 数学归纳法

使用情景：对于含有n(n∈N)的不等式类型

解题模板：第一步 验证当n取第一个值时不等式成立；

第二步 当n取第一个值时不等式成立，如果使不等式在n=k(n∈N)时成立的假设下，还能证明不等式在n=k+1也成立；

第三步 这个不等式对n取第一个值以后的自然数都能成立得出结论.

考点：数列与函数的综合；数列与不等式的综合.

方法六 换元法

使用情景：对于一般的不等式证明

解题模板：第一步 恰当的换元，适当的引入参数；

第二步 利用已知求出新元的取值范围；

第三步 根据现有的不等式放缩法得出结论.