特殊四边形+折叠

在学习平行四边形中，我们经常会遇见折叠类的题目，今天我们举例来分析这些题目的解法。

类型一、折叠后，使点与点重合

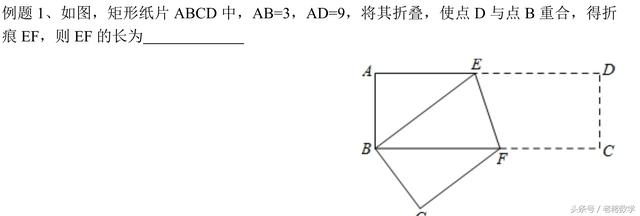
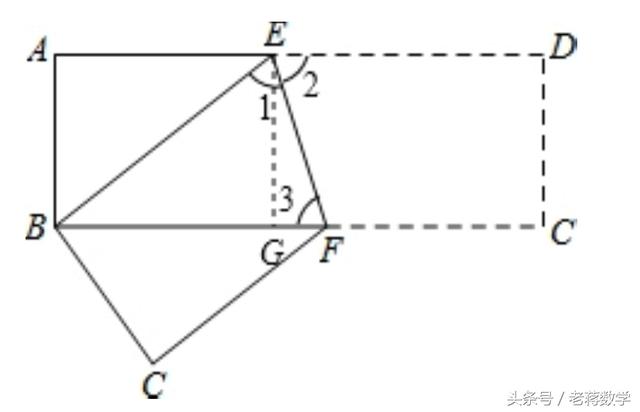
具体解题过程如下：

这里我们将图形进行简化，就会发现此类图形一般都含有以下元素：平行线+角平分线=等腰三角形

大家要记住这个简化图形，对你快速从复杂图形中找出有用信息有很大帮助！

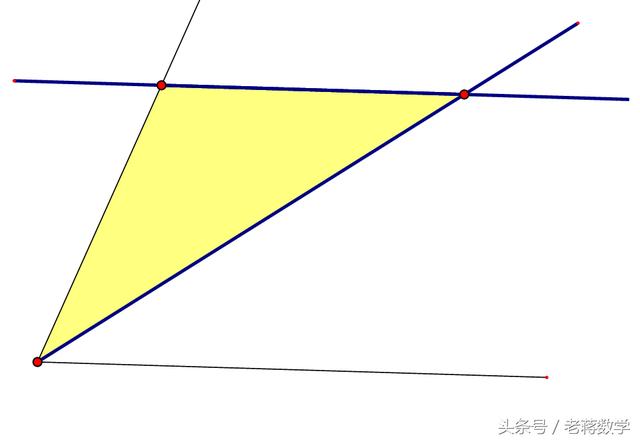
解题时候，用心观察，去繁留真，就会快速找到解题切入口。

二、折叠后，使点在某边上

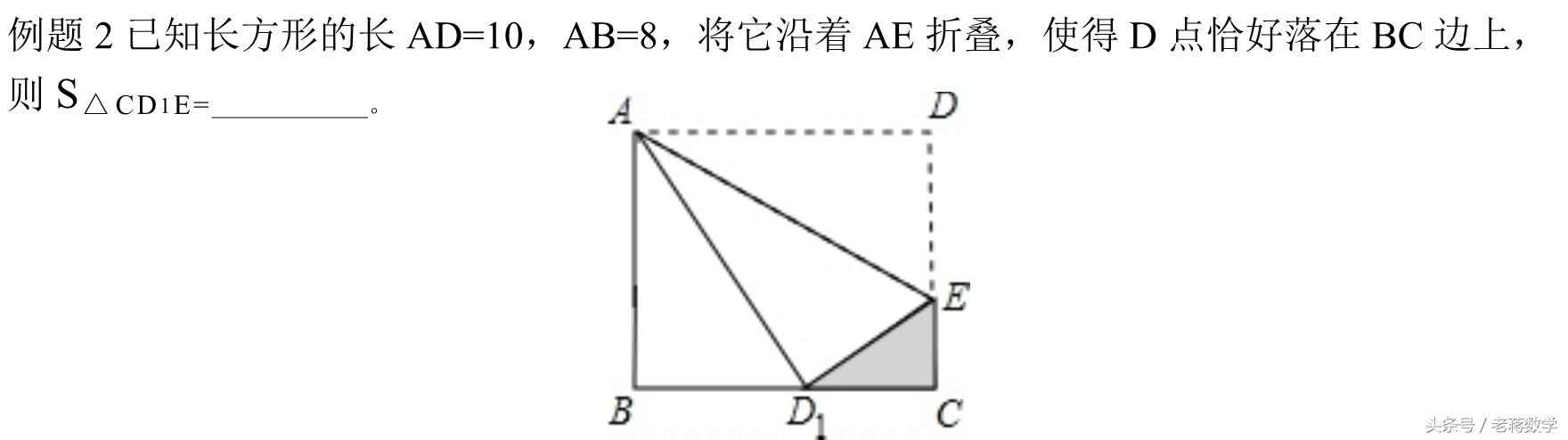
折叠后点在边上

此类问题大家一定要观察出到新位置的点与图形中边角组合又产生了什么图形，一般是三角形，有几个，这些因折叠产生出的新三角形，边、角可求否？是用勾股定理中：知二求一、还是知一求二？如果是知一求二型，设什么为未知数X,另一未知边证明用未知数表示，最后一般用勾股方程或者相似解决。

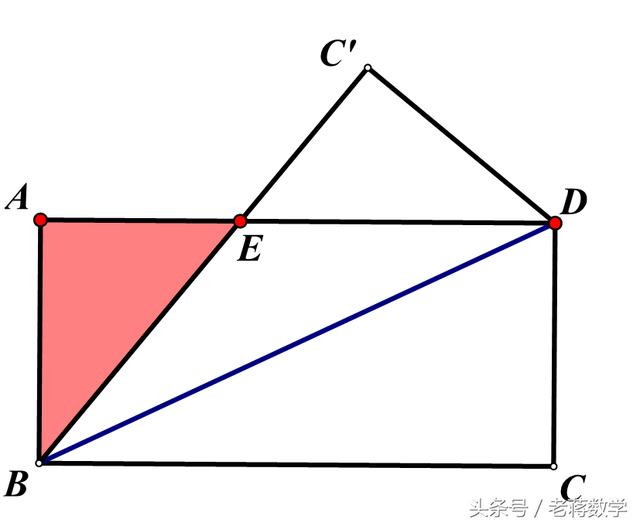
三、折叠后，使点在对角线上

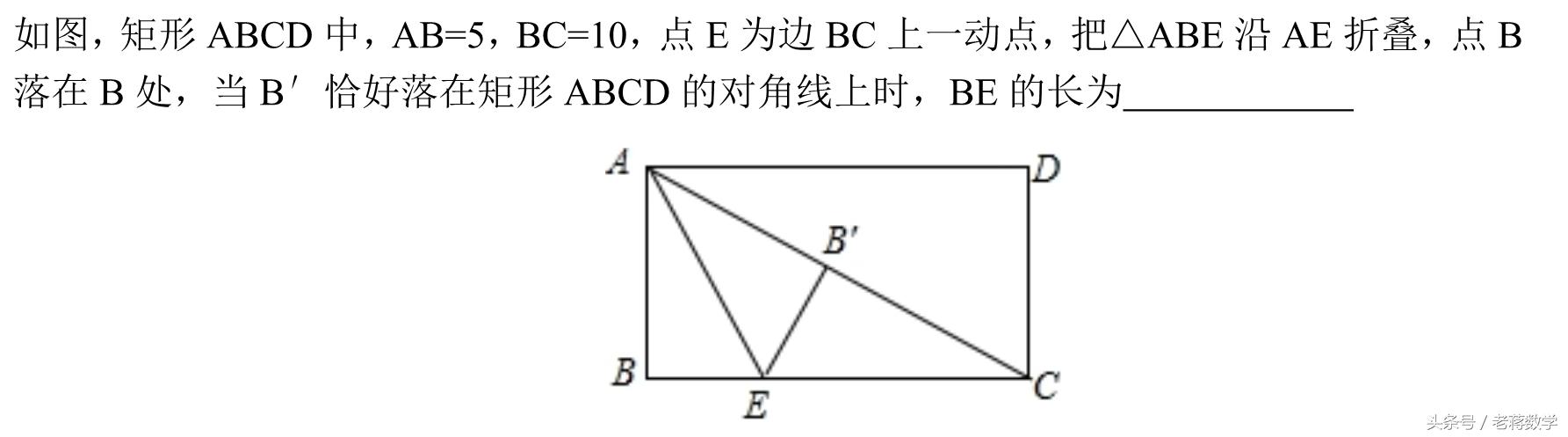
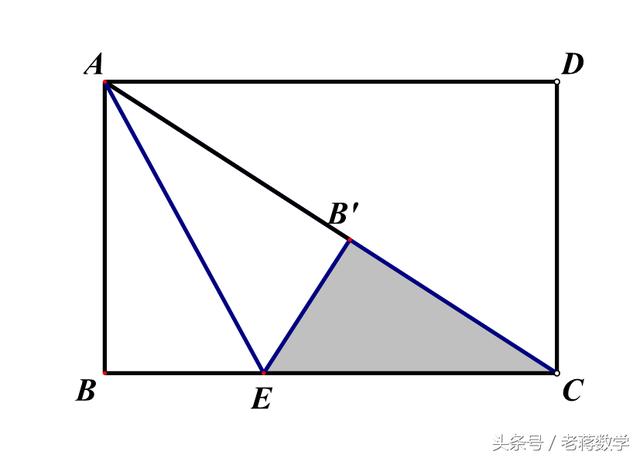
这种题目与类型二类似，折叠后经常会产生新直角三角形（下图阴影三角形），解决问题一般就在新产生的直角三角形中，用勾股方程来解决。

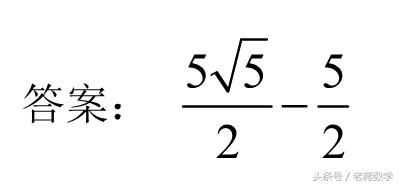
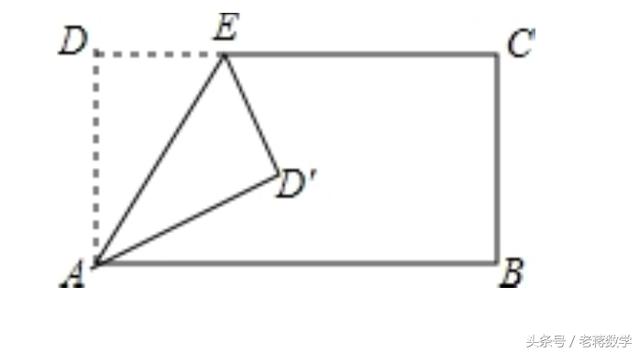
四、图形沿某直线折叠

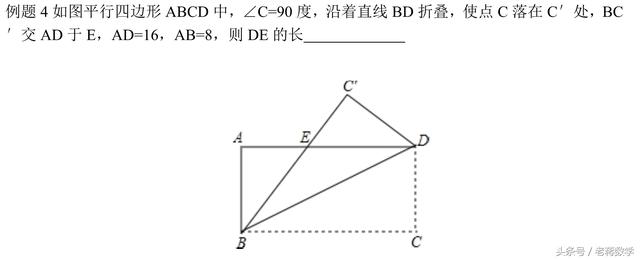
答案是10

这种问题，折痕即为角平分线，加上矩形对边平行，这里面有等腰三角形，可用等腰进行转化，最后和以上一样的处理方法，选择因折叠产生的新三角形，设合适的线段为未知数，用勾股定理就可解决。

好了，特殊的四边形（一般是矩形）折叠产生的求未知线段的题型，就介绍到这。你还有补充的吗？用一道题结束吧。聪明的你一定会解的出！