引例：

下题是补形法最简单的应用：

如图所示，在边长为6厘米的正方形内有一个三角形BEF，线段AE=3厘米，DF=2厘米。求三角形BEF的面积。

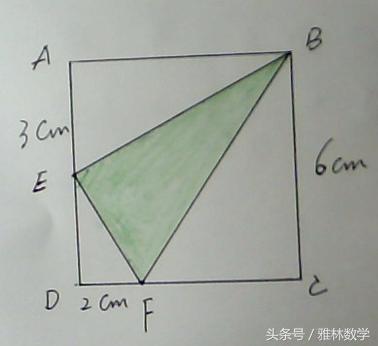
题图

解析：

图中三角形BEF为形状未知，所有边长未知，所有高未知。所以，尽管三角形是规则图形，我们还是把它当作不规则图形去求面积。用补形法。

这里不需要作图，因为需要补的图形都是现成的。

图形处理：

如下图做标记。

很明显，正方形ABCD的面积=①+②+③+S，在这个等式中，正方形的面积和①、②、③所标示的三角形面积均可求，所以，我们可以通过移项，用这些可求的面积去表示阴影部分的面积S：

S=正方形ABCD的面积-①-②-③

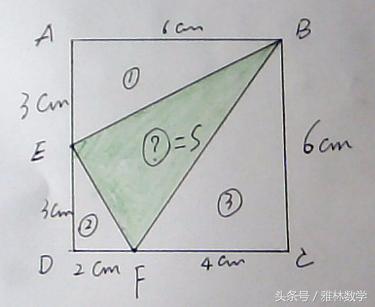
标示处理后的图形

补形法的应用举例：

如图所示，长方形的长和宽分别是6厘米和4厘米，阴影部分的总面积是10平方厘米。求四边形ABCD的面积。

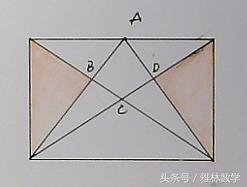
题图

解析：

如下对图形进行标示处理。

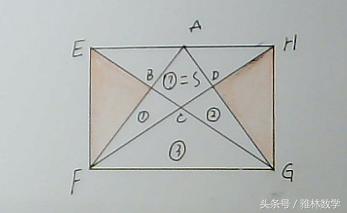
标示处理后的图形

因为四边形ABCD是个不规则四边形，所有边长未知，所有角度未知，所以直接求面积是不可能的。

在标示后的图形中，我们可以用三角形AFG的面积（①+②+③+S的和），减去①、②、③的和，即可的四边形ABCD的面积S的值。

上图中，三角形CEF的面积+三角形CGH-阴影部分的总面积，即可得到①+②的值，而③的值等于三角形AFG的一半，也等于长方形EFGH的四分之一，很容易求出。进而，S可求。

S=三角形AFG的面积-（①+②）-③

=6×4÷2-（6×4 ÷2-10）-6×4÷2 ÷2

=12-2-6

=4（平方厘米）

问题得解。

结束语

数学中的思想方法本身往往很简单，但在实际使用中却很灵活，有时因为使用环境被过度包装，甚至看不出来题目的本质，需要进行等价转化后才能露出本来面目。我们在实践中要善于进行等价转化，使问题符合既有模型，进而求解。