九年级数学，圆，相交弦定理

cc518学习网精品学习资料总目录

相交弦定理现在虽然在初中数学中已经不作要求了，但是如果能提前掌握这个知识，解题时还是会有一定优势的。

首先让我们来看看什么叫“相交弦定理”。

概念：圆内的两条相交弦，被交点分成的两条线段长的积相等。

几何语言：

若圆内任意弦AB、弦CD交于点P

则PA·PB=PC·PD（相交弦定理）

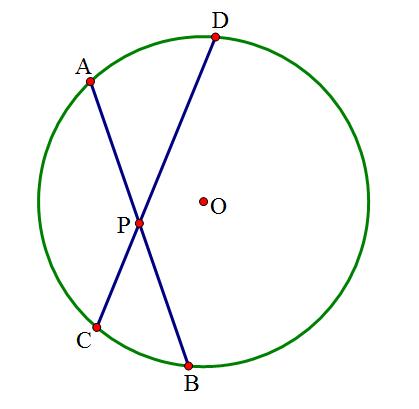
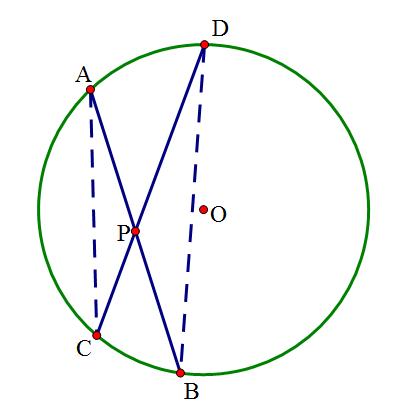
定理的证明：

连结AC，BD

由圆周角定理的推论，得∠A=∠D，∠C=∠B。

∴△PAC∽△PDB

∴PA∶PD=PC∶PB，PA·PB=PC·PD（若连结AD，BC也可证明）

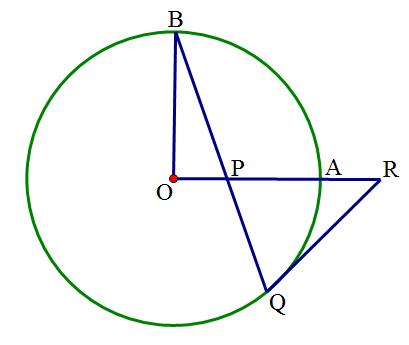
例题：如图，OA和OB是圆O的半径，并且OA⊥OB。P是OA上的任意一点，BP的延长线交圆O于点Q，点R在OA的延长线上，且RP=RQ.

求证：（1）RQ是圆O的切线；（2）OB·OB=PB·PQ+OP·OP

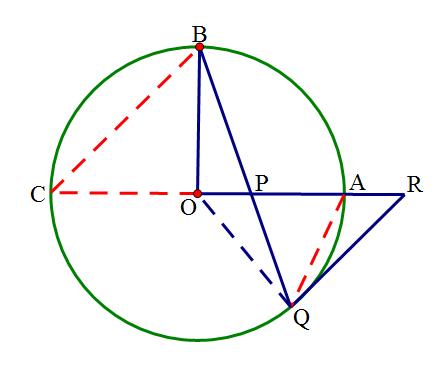
分析：（1）要证明切线无非是“连半径，证垂直”或“做垂直，证半径”，由于点Q已知在圆上，则属于“连半径，证垂直”。

（2）这种证明等量关系的题目，往往需要用到转化思想，这道题的关键在于PB·PQ要通过相交弦定理来转化！