一、基本模型：

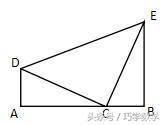
两个全等的三角形△ACD≌△BEC，拼成如图形状，使得A、C、B三点共线。

条件：△ACD≌△BEC

结论：1、△DCE是等腰直角三角形

2、AB=AD+BE

二、模型变形：

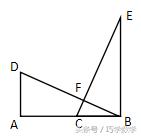
条件：△ABD≌△BEC

结论：1、BD⊥CE

2、AC=BE-AD

三、模型应用：

在下列各图中构造出三垂直模型：

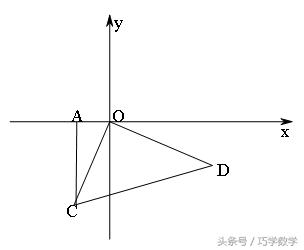
1、△OCD为等腰直角三角形

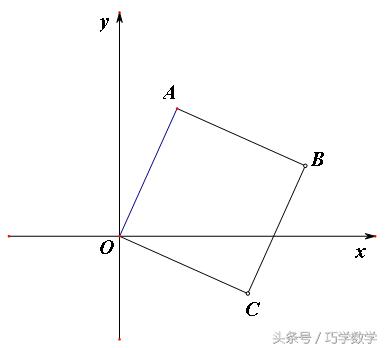
2、四边形OABC为正方形

“三垂直模型”是一个应用非常广泛的模型，它可以应用在三角形，矩形，平面直角坐标系，网格，一次函数，反比例函数，三角函数，二次函数以及圆等诸多的中考重要考点之中，所以掌握好这一模型会使你在中考中技高一筹，下面看一道典型例题，从这道题大家可以体会到“三垂直模型”的强大之处。

例题分析：

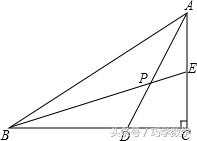
如图，在△ABC中，∠C=90°,D、E分别为BC、AC上一点，BD=AC，DC=AE，BE与AD交于点P，求∠ADC+∠BEC.

如图，过点B作BF⊥BC，且BF=AE=CD，连接AF，∠FBC=90°

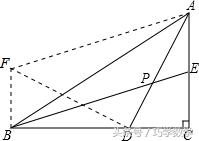
∴AC⊥BC，∠FBC=∠DCA．

∴BF∥AC，

∴四边形AFBE为平行四边形．

∴∠BFA=∠AEB．

在△BDF和△CAD中，

BF＝CD

∠FBC＝∠DCA

BD＝CA

∴△BDF≌△CAD（SAS）．

∴∠BFD=∠ADC，∠BDF=∠DAC，DF=DA．

∵∠ADC+∠DAC=90°，

∴∠ADC+∠BDF=90°，

∴∠ADF=90°，

∴∠DFA=∠DAF=45°．

∵∠AEB+∠BEC=180°，

∴∠AFB+∠BEC=180°，

∴∠BFD+∠DFA+∠BEC=180°，

∴∠ADC+∠AFD+∠BEC=180°，

∠ADC+∠BEC=135°．

故答案为：135．