高考数学，典型例题分析1：直线与直线之间的位置关系

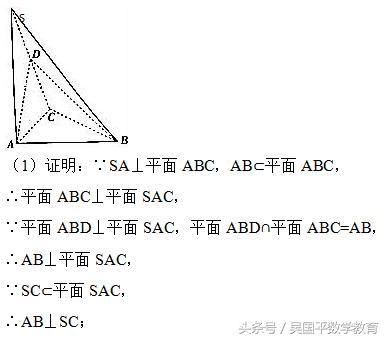
如图，在三棱锥S﹣ABC中，SA⊥平面ABC，点D是SC的中点，且平面ABD⊥平面SAC．

（1）求证：AB⊥SC；

（2）若SA=2AB=3AC，求二面角S﹣BD﹣A的正弦值．

考点分析：

二面角的平面角及求法；空间中直线与直线之间的位置关系．

在判断两条直线的位置关系时，首先应分析直线的斜率是否存在，两条直线都有斜率时，可根据斜率的关系作出判断，无斜率时，要单独考虑。

设两条直线的方程是l1：A1x＋B1y＋C1＝0，l2：A2x＋B2y＋C2＝0，两条直线的交点坐标就是方程组的解，若方程组有唯一解，则两条直线相交，此解就是交点坐标；若方程组无解，则两条直线无公共点，此时两条直线平行；反之，亦成立．

题干分析：

（1）根据线面垂直的判定定理和性质定理即可证明AB⊥SC；

在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理．

几个常用的结论：

过空间任一点有且只有一条直线与已知平面垂直。

过空间任一点有且只有一个平面与已知直线垂直。

（2）若SA=2AB=3AC，建立坐标系，求出平面的法向量即可求二面角S﹣BD﹣A的正弦值．