全国高中数学联赛平面几何题的证法探讨

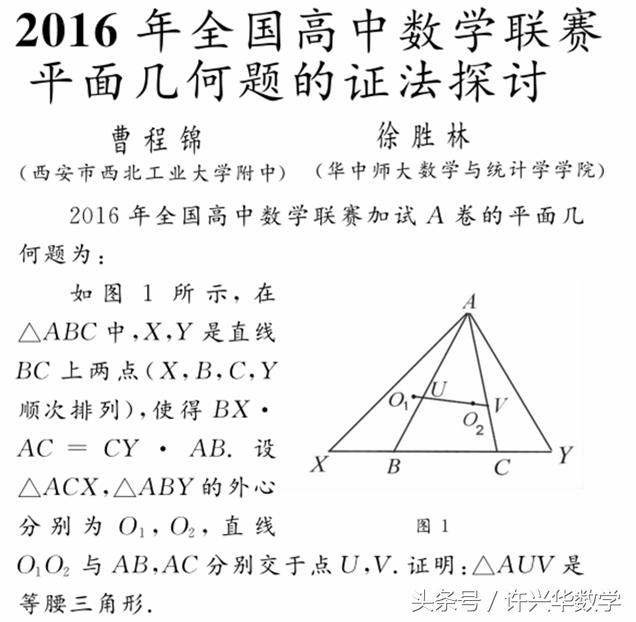
这道平面几何题以三角形和圆等基本图形为载体，考查四点共圆、相交弦定理、角平分线、相似三角形、全等三角形等基本知识点，对学生的逻辑推理能力要求较高 ．

本 文 探 讨 这 道 平面几 何试题的 证 明 方法，供大家参考 ．

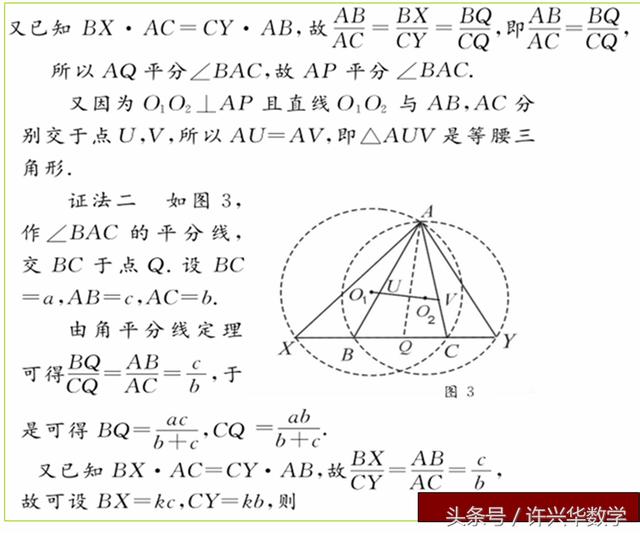
（许兴华数学）

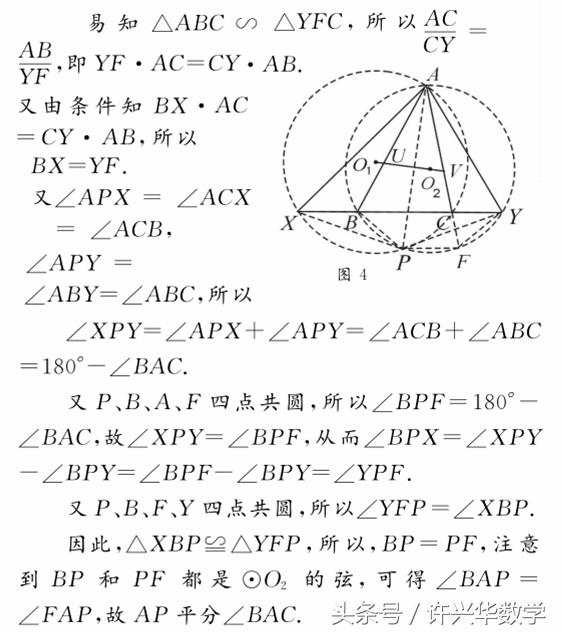
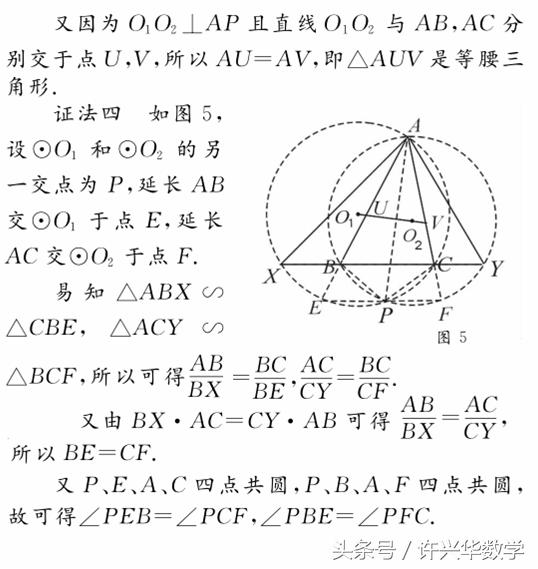
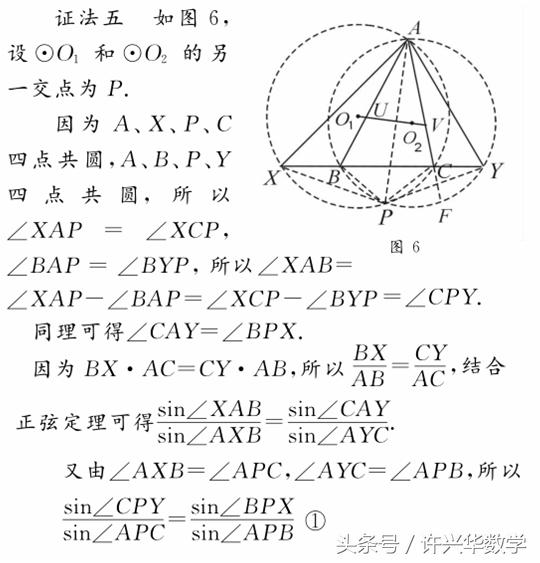
【评注】 涉及到证明角相等的问题，可以结合图形合理利用正弦定理实现转化，以算“代”证．

(许兴华数学)

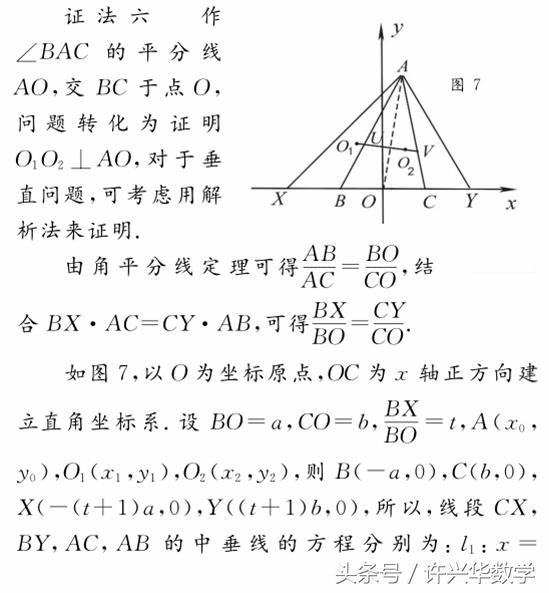
【评注】 证明平面几何问题的困难往往在于：添加合适的辅助线需要较强的技巧和较大的思维量．考虑到本题的图形特征和条件，合理建立直角坐标系，设参后表示出相关点的坐标，可以把问题转化为代数运算，也是一种好的处理策略．需要注意的是，能够用解析法解决的平面几何问题并不多，建议学生不要把解析法作为处理平面几何题的“法宝” ．

（许兴华数学）

进而利用外心的性质和圆的性质进行角的转化，通过构造相似三角形来完成证明．实际上，这一证法与命题组提供的证法二的思路是一致的．