考点一 集合的概念及运算
集合的运算性质及重要结论
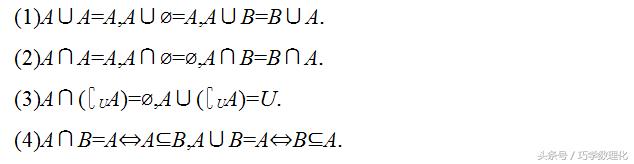


方法归纳
解答集合问题的思路
先正确理解各个集合的含义,认清集合元素的属性、代表的意义,再根
据元素的不同属性采用不同的方法对集合进行化简求解.
(1)若给定的集合是不等式的解集,用数轴求解;
(2)若给定的集合是点集,用数形结合法求解;
(3)若给定的集合是抽象集合或是用列举法表示的集合,用Venn图求解.
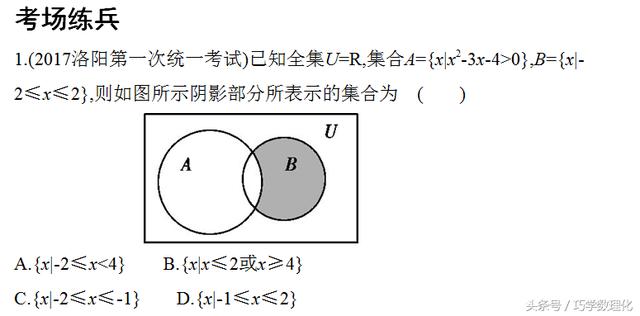
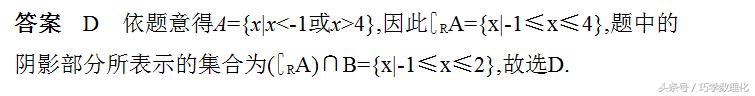


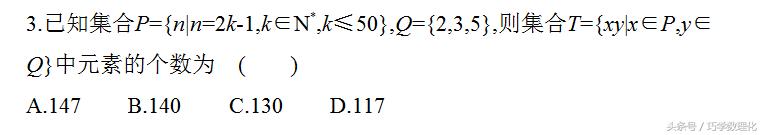

考点二 充分、必要条件的判断(高频考点)
命题点
1.充分、必要条件的判断.



方法归纳
充分、必要、充要条件的判断及应用的关注点
(1)要弄清先后顺序:“A的充分不必要条件是B”是指B能推出A,且A不
能推出B;而“A是B的充分不必要条件”是指A能推出B,且B不能推出A.
(2)要注意转化:¬p是¬q的必要不充分条件⇔p是q的充分不必要条件;
¬p是¬q的充要条件⇔p是q的充要条件.





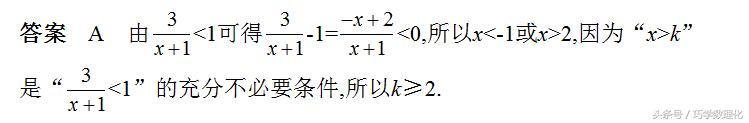
考点三 命题真假的判断与否定
1.四种命题的关系
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
2.全(特)称命题及其否定
(1)全称命题p:∀x∈M,p(x).它的否定¬p:∃x0∈M,¬p(x0).
(2)特称命题p:∃x0∈M,p(x0).它的否定¬p:∀x∈M,¬p(x).


方法归纳
含逻辑联结词的命题真假的等价关系
(1)p∨q真⇔p,q至少一个真⇔(¬p)∧(¬q)假.
(2)p∨q假⇔p,q均假⇔(¬p)∧(¬q)真.
(3)p∧q真⇔p,q均真⇔(¬p)∨(¬q)假.
(4)p∧q假⇔p,q至少一个假⇔(¬p)∨(¬q)真.
(5)¬p真⇔p假;¬p假⇔p真.

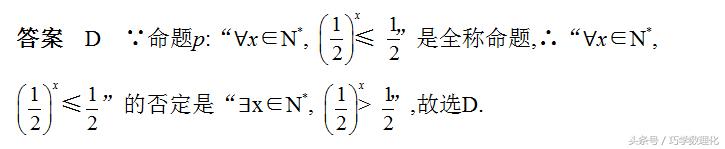






 加载中,请稍侯......
加载中,请稍侯......
精彩评论