中考数学探究性试题的解答策略

中考数学试卷中的探究性试题，因为综合程度高，解答时要用到众多

的数学思想方法，考生往往感到束手无策。现以某些省市中考数学探究性试题为例，谈谈这类问题的解答策略。

1.从“特殊”到“一般”，拾阶而上。

某些探究性试题一般给出几问，其中第一问在具体的数据或特殊情形下求解，其他几问则要求在一般情形下探究。解决问题的方法是：顺着解“特殊” 问题的思路，并注意 “一般”与“特殊”的转化，便能迎刃而解。

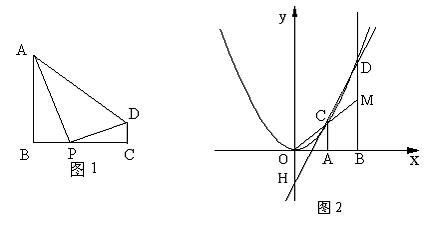
例1．如图1，AB⊥BC，DC⊥BC，垂足分别为B、C。

(1)当AB= 4，DC=1，BC= 4时，在线段BC上是否存在点P，使AP⊥PD？如果存在，求线段BP的长；如果不存在，请说明理由。

(2)设AB= a，DC=b，AD=c，那么，当a、b、c之间满足什么关系时，在直线BC上存在点P使AP⊥PD？

2．化“动”为“静”，分而治之。

有些以动态为情景的探究性试题，条件中涉及到点、线、面的运动，图形的全等、相似以及特殊三角形的关系。解决这类问题时，首先，化“动”为“静”，其次，根据运动的特征找准分类讨论的“临界点”，再则，有序的找出全等、相似以及特殊三角形中各种可能的“对应”，分别进行探究。

例3．如图3，在直梯形ABCD中，∠D=∠C=90°，AB=4，BC=6，AD=8。点P、Q同时从A点出发，分别作匀速运动，其中点P沿AB、BC向终点C运动，速度为每秒2个单位，点Q沿AD向终点D运动，速度为每秒1个单位。当这两个点达到自己的终点时，另一个点也停止运动，设这两个点从出发运动了t秒。

（1） 动点P与Q哪一点先达到自己的终点？此时t为何值？

（2） 当0＜t＜2时，求证：以PQ为直径的圆与AD相切

（3） 以PQ为直径的圆能否与CD相切？若有可能，求出t的值或t的取值范围；若不可能，请说明理由。