高中数学 二次函数 求最小值「必修一」「难点题」「干货」

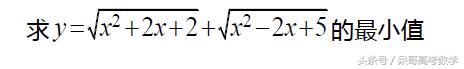
呆哥解析：这个题，如果直接左右平方，就略显复杂了，有个小细节，其实是在引导我们的，那就是以下的数据：

答案只会有三种情况：

1、没有。

分析：那就记下配方结论

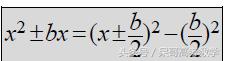
脑海中形成必要的配方“条件反射”

2、有想法，但是觉得麻烦，放弃了配方

分析：典型的动脑不动笔，考试中经常会有为难情绪而放弃了很多分数。需要培养“试错”精神。

3、进行了配方

第三种情况我们会走到下一步：

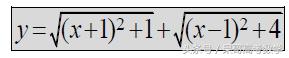
当然，1和4是一个非常完美的平方数：

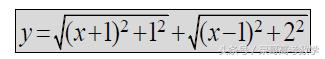
这个时候，如果我们会“无心插柳柳成荫”地想到了两点距离的结构，之所以这么说，是因为我们在前期的“试错”之时并不知道会出现这样的局面，只是说尝试了，发现有这样的一个趋势。

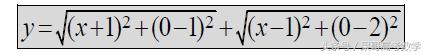
上面的式子，翻译成数学语言就是：

我们作图

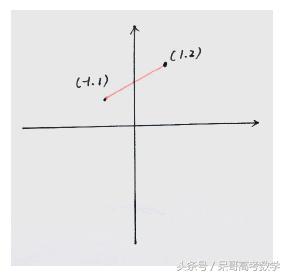
这个模型就是典型的初中两点一直线的最短距离问题，我们做点（-1,1）关于X轴对称的点（-1，-1），这个对称点与（1,2）的距离最短。【原理这里就不写了】

作图如下：

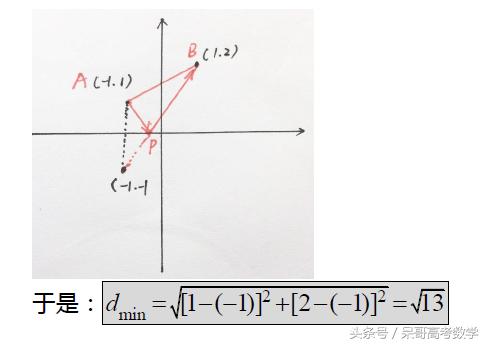
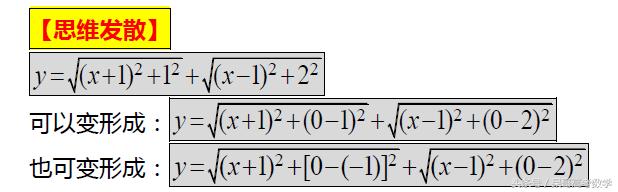
如果是变形成下面的形式，会发现其实就是算求：

x轴上的点到（-1，-1）和（1,2）两点的距离之和的最小值是多少？

显然，就是这两点的距离最短嘛，因为两点分布在X轴两侧。

于是：

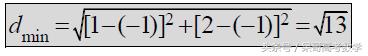
数学有时候就是这么好玩，不同的变形和思维，难易程度也会大不一样。