(2017年海南中考第18题)如图,AB是圆O的弦,AB=5,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是?
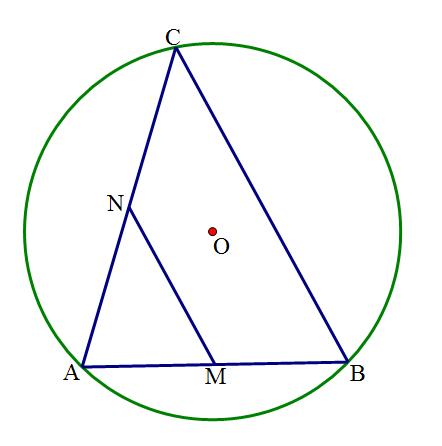
分析:本题从M、N分别是AB、AC的中点来进行突破,根据中位线定理可知:MN=1/2BC。所以要求MN的最大值,就是求BC的最大值。在圆中,显然BC为直径时最大。此时图形如下所示:
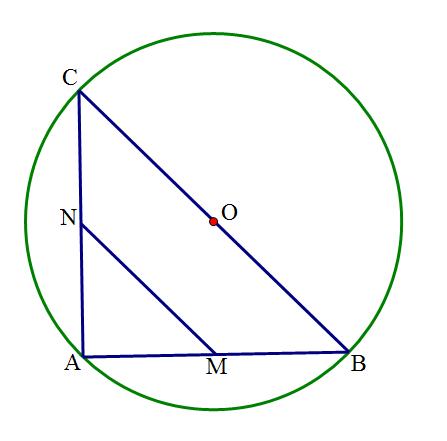
此时由于BC为直径,则∠A=90°,又因为已知∠ACB=45°,AB=5。则BC可求,答案如下图所示:
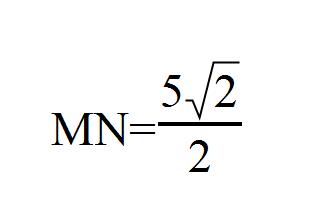
九年级数学,圆与中位线定理,这道题目难度适中
(2017年海南中考第18题)如图,AB是圆O的弦,AB=5,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是?

分析:本题从M、N分别是AB、AC的中点来进行突破,根据中位线定理可知:MN=1/2BC。所以要求MN的最大值,就是求BC的最大值。在圆中,显然BC为直径时最大。此时图形如下所示:

此时由于BC为直径,则∠A=90°,又因为已知∠ACB=45°,AB=5。则BC可求,答案如下图所示:
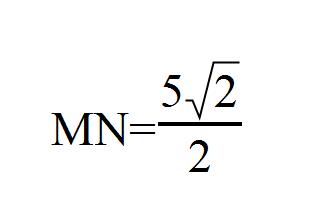
上一篇 : 人教七年级数学下开学入学检测试卷附答案
下一篇 : 初二下册数学丨频数与频率
初中数学,“将军饮马”的七大模型
人教版八年级数学上册第一章单元测试题(含答案)
初二《全等三角形》数学模型之“一线三等角”模型
 加载中,请稍侯......
加载中,请稍侯......
精彩评论