初中数学构造等腰三角形解题的辅助线做法
等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起考查。在许多几何问题中,通常需要构造等腰三角形才能使问题获解。那么如何构造等腰三角形呢?一般有以下四种方法:
(1)依据平行线构造等腰三角形;
(2)依据倍角关系构造等腰三角形;
(3)依据角平分线+垂线构造等腰三角形;
(4)依据120°角或60°角,常补形构造等边三角形。
1、依据平行线构造等腰三角形
例1:如图。△ABC中,AB=AB,E为AB上一点,F为AC延长线上一点,且BE=CF,EF交BC于D,求证DE=DF.
[点拔]:若证DE=DF,则联想到D是EF的中点,中点的两旁容易构造全等三角形,方法是过E或F作平行线,构造X型的基本图形,只需证两个三角形全等即可。
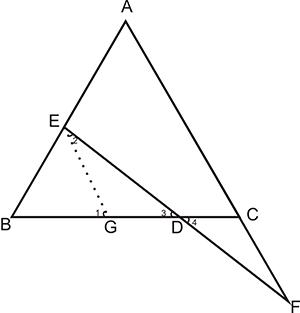
证明:过E作EG∥AC交BC于G
∴∠1=∠ACB,∠2=∠F
∵AB=AC
∴∠B=∠ACB
∴∠1=∠B
∴BE=GE
∵BE=CF
∴GE=CF
在△EDG和△FDC中
∠3=∠4
∠2=∠F
GE=CF
∴△EDG≌△FDC
∴DE=DF
[评注]:此题过E作AC的平行线后,构造了等腰△BEG,从而达到转化线段的目的。

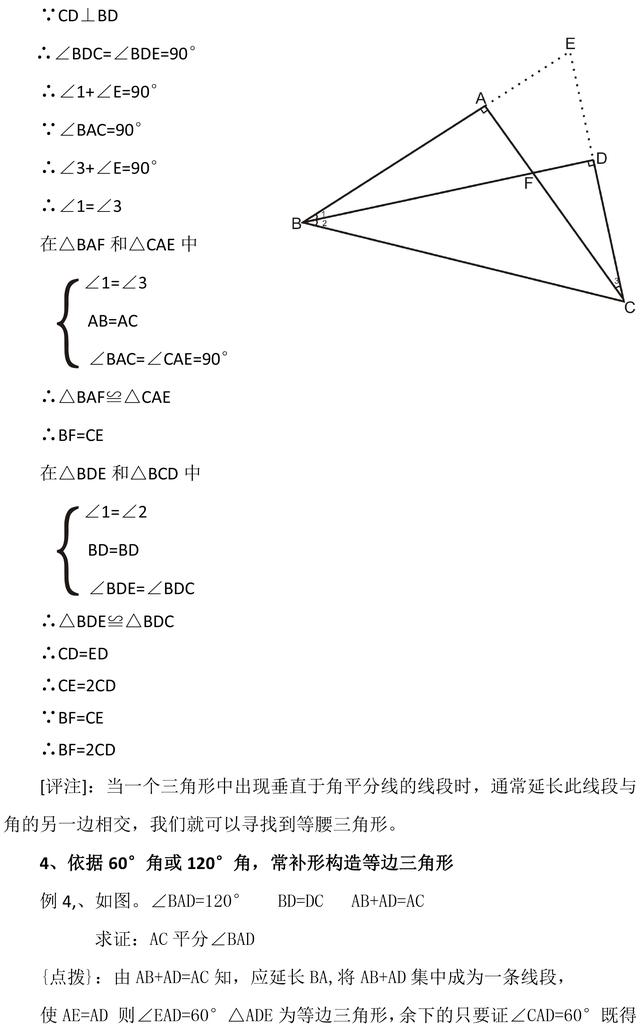
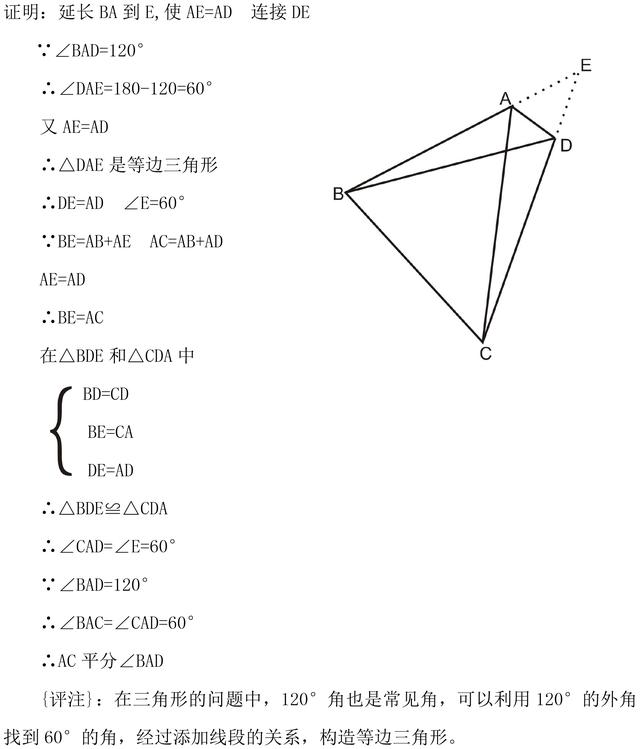
 加载中,请稍侯......
加载中,请稍侯......
精彩评论