九年级数学，等腰三角形与相似，如果有实力就来挑战这题吧

题目：如图，等腰△ABC中，AB=AC，D是边BC上一点，E是线段AD上一点，∠BED=2∠CED=∠BAC，求证：BD=2CD

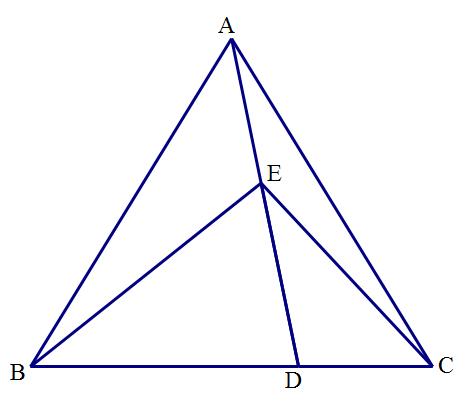
分析：构造相似三角形是关键

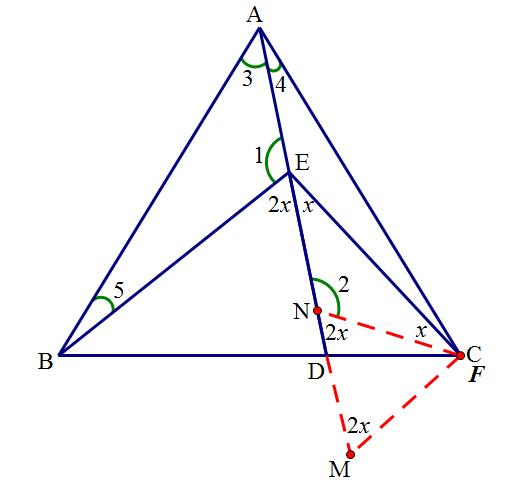
分析：作CM∥BE，交AD延长线于点M，截取CN=CM

则△BDE∽△CDM，BD：CD=BE：CM

因为∠BED=2∠CED，所以EN=CN，∠1=∠2

因为∠BED=∠BAC，所以∠5+∠3=∠3+∠4，所以∠4=∠5

因为AB=AC，所以△ABE≌△CAN（AAS）

所以AE=CN，BE=AN

因为AN=AE+EN=2CN=2CM=BE

所以 BE：CM=2 所以BD：CD=2,即BD=2CD 证毕

点评：此题还可利用三角形外心来解题，这里就不再赘述。