高考数学压轴 妙用函数的单调性解决最值问题的四大方法

【高考地位】

函数的单调性是函数的一个重要性质，几乎是每年必考的内容，例如判断和证明单调性、求单调区间、利用单调性比较大小、求值域、最值或解不等式．

【方法点评】

方法一 定义法

使用情景：一般函数类型

解题模板：第一步 取值定大小：设任意x1,x2∈D，且x1<x2；

第二步 作差：f(x1)-f(x2)；[来源:学科网]

第三步 变形（合并同类项、通分、分解因式、配方等）；

第四步 定符号；

第五步 得出结论.

考点：1.函数奇偶性的应用；2.利用定义法证明函数的单调性.

方法二 导数法

使用情景：较复杂的函数类型

解题模板：第一步 求函数f(x)的定义域；

第二步 求导f’(x)；

第三步 在定义域范围内解不等式f’(x)>0或f’(x)<0；

第四步 得出函数f(x)的增减区间.

方法三 复合函数分析法

使用情景：简单的复合函数类型

解题模板：第一步 先求函数的定义域；

第二步 分解复合函数，分别判断内外层函数的单调性；

第三步 根据同增异减，确定原函数的增减区间.

考点：待定系数，导数与单调区间．

方法四 图像法

使用情景：图像比较容易画出的函数类型

解题模板：第一步 通过题目条件画出函数图像；

第二步 从图像中读出函数的单调区间.

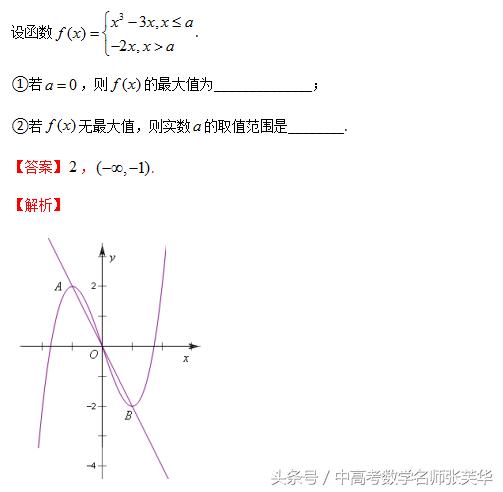
考点：1.分段函数求最值；2.数形结合的数学思想.

【名师点睛】1.分段函数的函数值时，应首先确定所给自变量的取值属于哪一个范围，然后选取相应的对应关系．若自变量值为较大的正整数，一般可考虑先求函数的周期．若给出函数值求自变量值，应根据每一段函数的解析式分别求解，但要注意检验所求自变量的值是否属于相应段自变量的范围；2.在研究函数的单调性时，常需要先将函数化简，转化为讨论一些熟知的函数的单调性，因此掌握一次函数、二次函数、幂函数、对数函数等的单调性，将大大缩短我们的判断过程．