数形结合，巧解二次函数选择题

数学选择题在命制时便考虑到的思维的特殊性，通常解法有正面推导、代入答案、排除法等，全部掌握需要一定时间，只有多做题，才能慢慢领悟这些方法的妙用，下面用一道二次函数选择题来说明利用数形结合巧解选择题。

如图，抛物线y=ax²+bx+c（a≠0）过点（1，0）和（0，-2），且顶点在第三象限，设P=a-b+c，则P的取值范围是（ ）A.-4<P<0 B.-4<P<-2 C.-2<P<0 D.-1<P<0

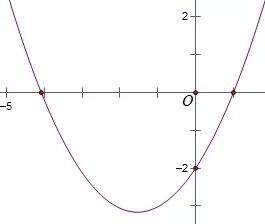
从学生完成过程中的思维活动来看，基本上拿到此题，都能将两个点坐标代入函数解析式，从而得到a+b+c=0和c=-2这两个结论，更进一步的结果是a+b=2，然后就由顶点在第三象限想到顶点坐标均为负数，想到列两个不等式，然后……就没有然后了，全开始卡壳。本题是一道选择题，所以解析法用在它身上无疑是会花费大量时间的，因此我们得认真观察图形，结合我们所学的二次函数的图象特征来分析它：

第一个要关心的是它的开口方向，由图中可知，此时开口向上，顶点在第三象限，想像一下函数开口变大，那么a值应该变小，最小可以变成多少呢？当a值小到接近0时，二次函数图象会接近一条直线（经过上述那两个已知点），顶点若在这条直线下方，那么开口方向就不再向上了，而变成向下，此时顶点就不在第三象限了；继续刚才的想像，开口变小，那么a值应该变大，最大能变成多少呢？当a值变大时，其对称轴会接近y轴，顶点也接近y轴，由于第三象限的限制，故此它的顶点最多只能接近（0，-2）。

基于以上两个数形结合的动态想像（此时不宜演示给学生看动画），开始我们的解析：将函数解析式化为y=ax²+(2-a)x-2，考虑它变化的两个极限情况，当二次函数成为一条直线（一次函数）时，a=0，解析式为y=2x-2；当顶点在（0，-2）时 ，2-a=0，a=2，解析式为y=2x²-2；

最后再来看P=a-b+c，这个式子是点（-1，a-b+c）的纵坐标，理解为当横坐标为-1时二次函数的函数值。将x=-1分别代入上面的两个函数解析式，分别计算出P=-4和P=0，所以范围是-4<P<0

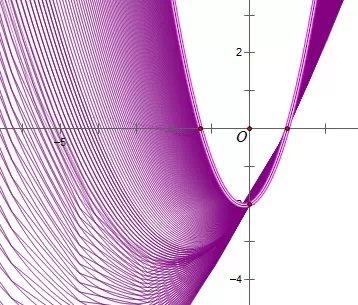
最后放一个动画截图，显示了二次函数图象当a变化时图象的轨迹，帮助学生来完成理解。