中考数学基础综合题讲解分析：二次函数的基本应用

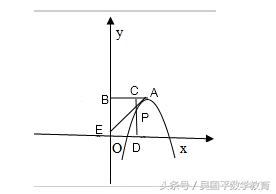
已知抛物线y=﹣x2+2mx﹣m2+2的顶点A在第一象限，过点A作AB⊥y轴于点B，C是线段AB上一点（不与点A、B重合），过点C作CD⊥x轴于点D并交抛物线于点P．

（1）若点C（1，a）是线段AB的中点，求点P的坐标；

（2）若直线AP交y轴的正半轴于点E，且AC=CP，求△OEP的面积S的取值范围．

解：（1）依题意得顶点A的坐标为（2，a），

设P（1，n）据x=﹣b/2a，得A点的横坐标为m，即m=2，

所以y=x2+4x﹣2，把P点的坐标代入得n=1，

即P点的坐标为（1，1）

（2）把抛物线化为顶点式：y=﹣（x﹣m）2+2，

可知A（m，2），设C（n，2），

把n代入y=﹣（x﹣m）2+2得y=﹣（n﹣m）2+2，

所以P（n，﹣（n﹣m）2+2）

∵AC=CP

∴m﹣n=2+（m﹣n）2﹣2，

即m﹣n=（m﹣n）2，

∴m﹣n=0或m﹣n=1，

又∵C点不与端点A、B重合

∴m≠n，

即m﹣n=1，

则A（m，2），P（m﹣1，1）

由AC=CP可得BE=AB

∵OB=2

∴OE=2﹣m，

∴△OPE的面积

S=（2﹣m）（m﹣1）/2

=﹣（m﹣3/2）2+1/8（1＜m＜2），

∴0＜S＜1/8．

考点分析：

二次函数综合题。

题干分析：

（1）根据题意得顶点A的坐标为（2，a），然后设P（1，n）代入x=﹣b/2a，得A点的横坐标为m，求得函数的解析式，把P点的坐标代入得n=1，从而求得函数的解析式；

（2）把抛物线化为顶点式：y=﹣（x﹣m）2+2，求得其顶点坐标，设C（n，2），然后表示出P（n，﹣（n﹣m）2+2）根据AC=CP求得m﹣n的值，然后表示出OB、OE的值从而表示出△OPE的面积，进而求得面积的取值范围。

解题反思：

本题考查了二次函数的应用，解题的关键是正确的用字母表示出点的坐标，并利用题目的已知条件得到有关的方程或不等式，从而求得未知数的值或取值范围。