填空题是高考数学最重要的题型之一，收好这些解题方法，战胜高考

高考数学填空题，典型例题分析1：

若函数y=f（x）在实数集R上的图象是连续不断的，且对任意实数x存在常数t使得f（x+t）=tf（x）恒成立，则称y=f（x）是一个“关于t的函数”，现有下列“关于t函数”的结论：

①常数函数是“关于t函数”；

②正比例函数必是一个“关于t函数”；

③“关于2函数”至少有一个零点；

④f（x）=（1/2）x是一个“关于t函数”．

其中正确结论的序号是　 　．

解：①对任一常数函数f（x）=a，存在t=1，有f（1+x）=f（x）=a，

即1•f（x）=a，所以有f（1+x）=1•f（x），

∴常数函数是“关于t函数”，故①正确，

②正比例函数必是一个“关于t函数”，设f（x）=kx（k≠0），存在t使得f（t+x）=tf（x），

即存在t使得k（x+t）=tkx，也就是t=1且kt=0，此方程无解，故②不正确；

③“关于2函数”为f（2+x）=2•f（x），

当函数f（x）不恒为0时，有f(2+x)/f(x)=2＞0，

故f（x+2）与f（x）同号．

∴y=f（x）图象与x轴无交点，即无零点．故③错误，

④对于f（x）=（1/2）x设存在t使得f（t+x）=tf（x），

即存在t使得（1/2）t+x=t（1/2）x，

也就是存在t使得（1/2）t（1/2）x=t（1/2）x，

也就是存在t使得（1/2）t=t，此方程有解，故④正确．

故正确是①④，

故答案为①④．

考点分析：

函数的连续性．

题干分析：

根据抽象函数的定义结合“关于t函数”的定义和性质分别进行判断即可。

解题反思：

本题主要考查抽象函数的应用，利用函数的定义和性质是解决本题的关键。

填空题虽然数量上不多，但要想在高考数学中获得优异的成绩，那么大家一定要尽量全拿填空题的分数，保证客观题的分数拿到手，这样才能获得考试基本分，为后面解决大题奠定良好的基础。

同时，大家在思想上不能轻视填空题，一定要努力提高基础知识和基本技能，提高推理或运算能力等。

下面我们介绍一些常见的填空题解题方法，具体如下：

填空题解题方法一、直接法

它是直接从题设条件出发、利用定义、定理、性质、公式等知识，通过变形、推理、运算等过程，直接得到结果，可以说这是解填空题的基本方法。

填空题解题方法二、数形结合法

由于填空题不必写出论证过程，因而画出辅助图象、方程的曲线或借助表格等进行分析并解答，这是一种数形结合的解题方法。

填空题解题方法三、 特殊化法

当填空题暗示，答案只有一个“定值”时，我们可以取一些特殊化法(代特殊值、位置、图形，构造数学模型等)来确定这个“定值”，特别适用于题目的条件是一般性的角度给出的问题。

高考数学填空题，典型例题分析2：

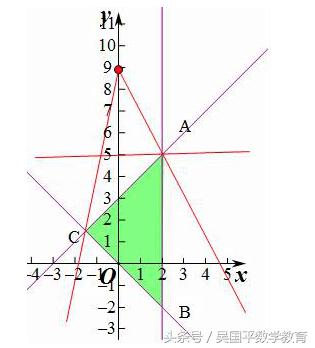
考点分析：

简单线性规划。

题干分析：

作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合以及分类讨论的思想进行求解即可。

解题反思：

本题主要考查线性规划的应用，根据目标函数的几何意义，利用数形结合是解决本题的关键．注意本题要对k进行分类讨论。

填空题解题方法四、待定系数法

待定系数法是一种常用的数学方法，对于某些数学问题，如果已知所求结果具有某种确定的形式，则可引进一些尚待确定的系数来表示这种结果，通过已知条件建立起给定的算式和结果之间的恒等式，得到以待定系数为元的方程（组）或不等式（组），解之即得待定的系数。

填空题解题方法五、等价转化法

指将所给问题等价转化为另一种容易理解的语言或易求解的形式。

填空题解题方法六、巧用结论

由于填空题不必写出过程，故利用常用的结论，可简化解题。

填空题解题方法七、特征分析法)

有些问题看似非常复杂，一旦挖掘其隐含的数量或位置等特殊关系，则问题或迎刃而解。

近几年高考数学填空题相继出现了阅读理解、发散开放、多项选择、实际应用等题型，对学生的思维能力和分析问题、解决问题的能力提出了更高要求。因此，我们必须要掌握好一些解答填空题的方法和策略。

高考数学填空题，典型例题分析3：

若α，β∈[﹣π/2，π/2]，且αsinα﹣βsinβ＞0，则下列关系式：①α＞β；②α＜β；③α+β＞0；④α2＞β2；⑤α2≤β2

其中正确的序号是：　 　．

解：令f（x）=xsinx，x∈[﹣π/2，π/2]，

∵f（﹣x）=﹣x•sin（﹣x）=x•sinx=f（x），

∴f（x）=xsinx，x∈[﹣π/2，π/2]为偶函数．

又f′（x）=sinx+xcosx，

∴当x∈[0，π/2]，f′（x）＞0，即f（x）=xsinx在x∈[0，π/2]单调递增；

同理可证偶函数f（x）=xsinx在x∈[﹣π/2，0]单调递减；

∴当0≤|β|＜|α|≤π/2时，f（α）＞f（β），即αsinα﹣βsinβ＞0，反之也成立，

∴α2＞β2．

故答案为④．

考点分析：

三角函数线。

题干分析：

构造函数f（x）=xsinx，x∈[﹣π/2，π/2]，利用奇偶函数的定义可判断其奇偶性，利用f′（x）=sinx+xcosx可判断f（x）=xsinx，x∈[0，π/2]，与x∈[﹣π/2，0]上的单调性，从而可选出正确答案。

考生要想在高考数学中拿到填空题的分数，那么大家就必须要学会和掌握好准确、严谨、全面、灵活运用知识的能力和基本运算能力，解题时必须按照规则进行切实的计算和合乎逻辑的推理、计算。

最后记住解决高考数学填空题四个注意事项：审题要仔细，要求要看清，书写要规范，小题巧做。