八年级数学，一次函数与三角形面积

一次函数的题目经常需要求函数解析式，但是有时候函数解析式的运算会较为复杂。

例：如图，在平面直角坐标系xOy中，已知点A（1，m+1），B（a，m+1），C（3，m+3），D（1，m+a），m>0，1<a<3点P（n-m，n）是四边形ABCD内的一点，且△PAD与△PBC的面积相等，求n-m的值。

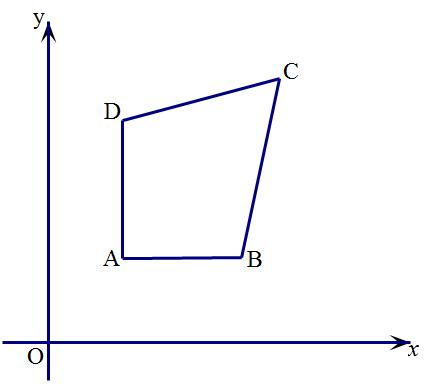
题目图形

分析：审题时应该注意到点A，点D的横坐标相同，所以AD∥y轴，同理AB∥x轴。由于P点在四边形ABCD内部，故我们可以先画出图形。

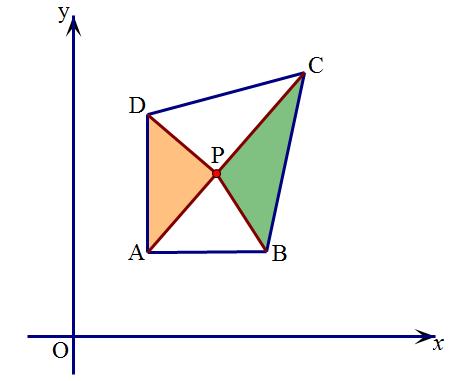
分析：要求n-m的值就必须根据△PAD与△PBC的面积相等来列出等量关系。由图形可知△PAD的面积易求，△CPB的面积则需要用到：“水平宽和铅直高”，这种求三角形面积的方法在整个初中阶段非常重要，务必要掌握。

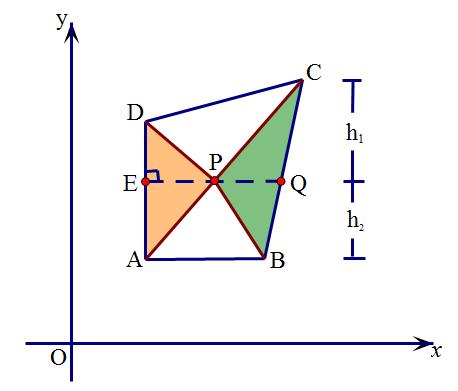
分析：此时就必须求出BC函数解析式，根据Q点和P点纵坐标相同，求出PQ的长。

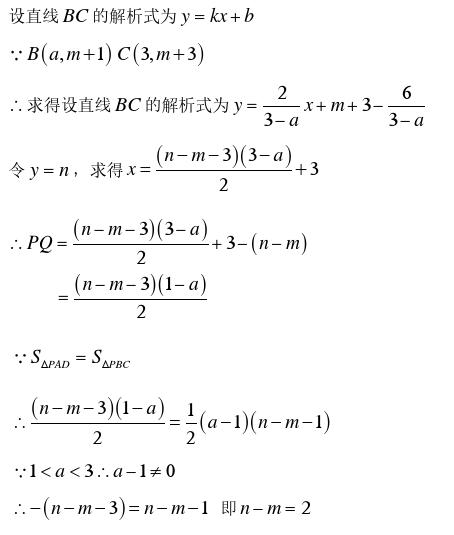
点评：此题思路简单，着重考察含字母的运算能力。