考点1 : 空间几何体的三视图、表面积、体积
【例1】我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器------商鞅铜方升,其三视图如图所示(单位:寸),若取3,其体积为12.6(立方寸),则图中的为____________.
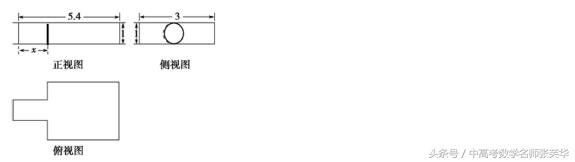
分析:以三视图为载体考查几何体的体积,解题的关键是根据三视图想象还原几何体的形状构成,并从三视图发现几何中各元素间的位置关系及数量关系,然后在直观图中求解.在求几何体的体积时,若给定的几何体是规则柱体,锥体或台体,可直接利用公式求解.若所给的几何体的体积不能直接利用公式得出,常用转换法,分割法,补形法等求解.
【答案】1.6
【规律方法】1、画三视图的基本原则是:长对正,宽相等,高平齐.在做题时也要根据这个原则来画直观图.要根据这个原则来验证所画直观图是否正确.
2、三视图问题关键是搞清楚三视图中的每条轮廓线代表的意义,三视图中给出的尺寸在几何体中对应哪些线段的尺寸,三视图中的角度在几何体对应的角度是多少.尤其要注意图中的直角,这是一个很重要的信息.必须结合三视图弄清几何体的直观图的构成,根据三视图的信息确定直观图中相关的量,然后才能进行相关计算.
3、求几何体体积问题,可以多角度、多方位地考虑问题.在求三棱锥体积的过程中,等体积转化法是常用的方法,转换底面的原则是使其高易求,常把底面放在已知几何体的某一面上.
4、求不规则几何体的体积,常用分割或补形的思想,将不规则几何体变为规则几何体,易于求解.
考点2 : 球与多面体

【规律方法】1、涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系.
2、求与球有关的“切”或者“接”球半径时,往往用到的方法有构造法或者直接确定球心.
3、求三棱锥的体积要注意如何选取底面和顶点.因为三棱锥的每一个面都可以作为底面,每一个顶点都可以作为顶点.
考点3 :线面位置关系的命题真假判断

【规律方法】解决空间点、线、面位置关系的组合判断题,主要是根据平面的基本性质、空间位置关系的各种情况,以及空间线面垂直、平行关系的判定定理和性质定理进行判断,必要时可以利用正方体、长方体、棱锥等几何模型辅助判断,同时要注意平面几何中的结论不能完全移植到立体几何中.
考点4 :空间中的线、面位置关系的判定与性质
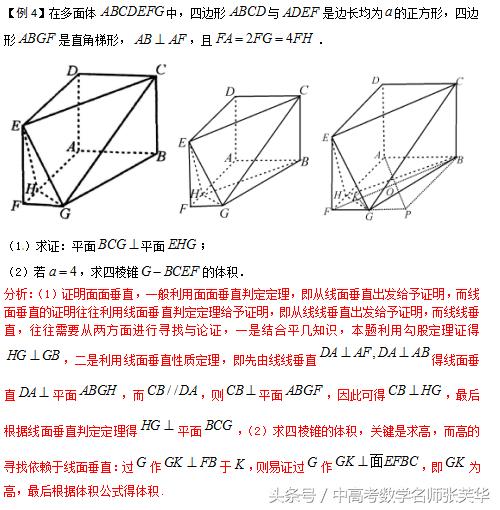
【规律方法】1、证明线面垂直,就考虑证明直线垂直平面内的两条相交直线;而证明异面的线线垂直,很多题都要通过线面垂直来证明;对相交直线垂直的证明,一般考虑用平面几何里的方法.常见的有以下几种,若是等腰三角形,则底边上的中线与底边垂直;若是锥形、菱形(正方形),则对角线互相垂直;若是矩形,则邻边互相垂直;
若告诉了线段的长度,或者是告诉了边与边之间的关系,则用勾股定理.
2.线面、线线垂直与平行的位置关系在面面平行与垂直位置关系的证明中起着承上启下的桥梁作用,依据线面、面面位置关系的判定定理与性质定理进行转化是解决这类问题的关键.证明面面平行主要依据判定定理,证明面面垂直时,关键是从现有直线中找一条直线与其中一个平面垂直,若图中不存在这样的直线应借助添加中线、高线等方法解决.
考点5: 空间距离和角

【规律方法】1、异面直线所成的角,通过作平行线,转化为相交直线所成的角.具体地,有以下两种方法:一是在其中一条上的适当位置选一点,过该点作另一条的平行线;二是在空间适当位置选一点,过该点作两条异面直线的平行线.求异面直线所成的角,点的选取很重要.2、直线与平面所成的角就是直线与其在该平面内的射影所成的角.求线面角的关键是找出斜线在平面内的射影,一般在斜线上的某个特殊的位置找一点,过该点平面的垂线,从而作出射影;3、作二面角的平面角,有以下两种方法,一是在棱上适当位置取一点,过该点分别在两个面内作棱的垂线;二是通过作棱的垂面来作.二面角是理科数学的重点考查内容,必须予以高度重视.4、求点到平面的距离除直接作出面的垂线外,常常用到等体积法.5、求空间的角与距离,总的原则是转化到同一平面内在三角形中进行求解.
考点6 :折叠问题

【规律方法】(1)解决折叠问题的关键是搞清翻折前后哪些位置关系和数量关系改变,哪些不变,抓住翻折前后不变的量,充分利用原平面图形的信息是解决问题的突破口.(2)把平面图形翻折后,经过恰当连线就能得到三棱锥、四棱锥,从而把问题转化到我们熟悉的几何体中解决.
考点7 :立体几何的探索性问题

【规律方法】解决探究某些点或线的存在性问题,一般方法是先研究特殊点(中点、三等分点等)、特殊位置(平行或垂直),再证明其符合要求,一般来说是与平行有关的探索性问题常常寻找三角形的中位线或平行四边形.
对于是否存在问题,首先要分析条件,看结论需要的条件已有哪些,分析欲使结论成立,还需要什么条件,结合所求,不难作出辅助线.
考点8 :利用空间向量求角与距离问题

【规律方法】1、运用空间向量坐标运算求空间角的一般步骤:①建立恰当的空间直角坐标系;②求出相关点的坐标;③写出向量坐标;④结合公式进行论证、计算;⑤转化为几何结论.
2.建立空间直角坐标系时,一定要注意三轴是否两两互相垂直(有的学生斜线也拿来作为Z轴);
3.证线线垂直,只需它们的方向向量的数量积为0即可;
4.两异面直线所成的角不一定是直线的方向向量的夹角;两平面的法向量的夹角与二面角相等或互补;直线的方向向量与平面的法向量的夹角与线面角的余角相等或互补.
5.用向量求二面角有以下两种方法,一是过棱上的点(不一定是同一个点)分别在两个面内作垂直于棱的向量,然后求这两个向量的夹角,二是求两个面的法向量的夹角;
6.直线与平面所成的角的正弦等于直线与平面的法向量的夹角的余弦的绝对值.
7.用空间向量求点到平面的距离的方法步骤是:(1)求出平面的法向量n;(2)任取一条过该点的该平面的一条斜线段,求出其向量坐标n1;(3)求点到平面的距离
 加载中,请稍侯......
加载中,请稍侯......
精彩评论