方法一、函数法

(1)利用已知函数性质求最值.

已知函数解析式，直接利用已知的基本初等函数的性质（最值、单调性、奇偶性等）是函数法的主要类型之一．

(2)构建函数模型求最值

很多最值问题需要先建立函数模型，再利用函数性质求解．建立函数模型的关键是找到一个变量，利用该变量表达求解目标，变量可以是实数，也可以是角度（弧度实际上也可以看作一个实数），建立函数模型需要注意建立的函数模型的定义域．

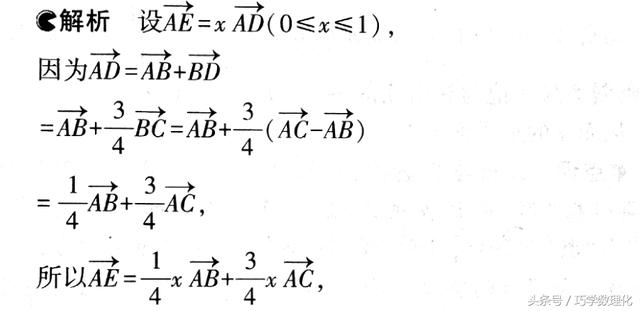
点评

已知E点在线段AD上移动，利用共线向量定理设出变量x，建立求解目标关于x的函数关系后利用函数性质求解．

方法二、不等式法

(1)利用基本不等式求最值.

基本不等式法是求最值的常用方法之一，使用基本不等式时要注意：

①基本不等式的使用条件和等号是否能够成立；

②变换已知不等式使之符合使用基本不等式的条件．

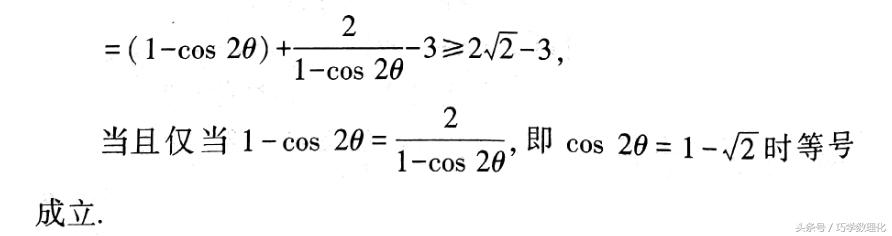
(2)建立求解目标的不等式求最值.

把求解目标归入一个不等式，通过解不等式得出目标最值，是求最值的常用方法之一，在解析几何中求离心率的最值、一般问题中求参数最值时经常使用.

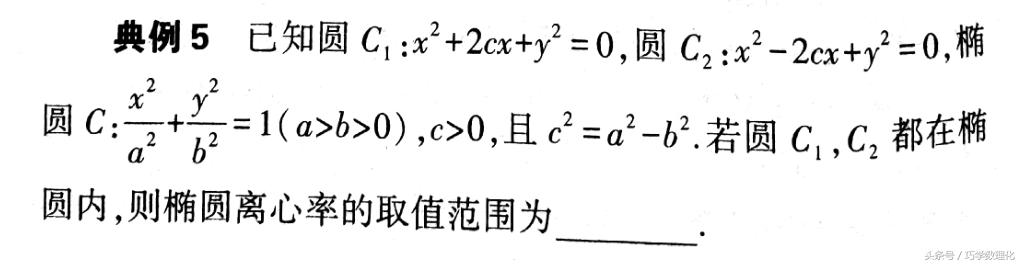
方法三、导数法

(1)直接使用导数求最值.

三次函数、指数、对数与其他函数综合的函数求最值时要利用导数法．

基本步骤：确定单调性和极值，结合已知区间和区间的端点函数值确定最值．

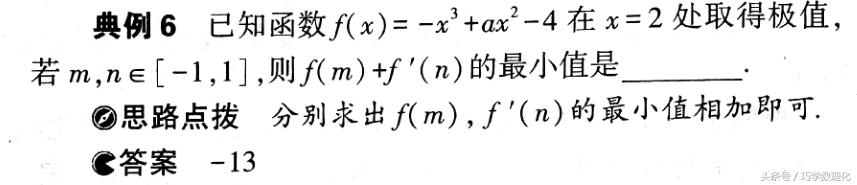
(2)构造函数利用导数求最值

不等式恒成立问题的一个基本处理方法是转化为函数最值问题，需要通过构造函数求函数最值，而求函数最值时导数方法最有效．注意使用导数求函数最值的基本步骤．

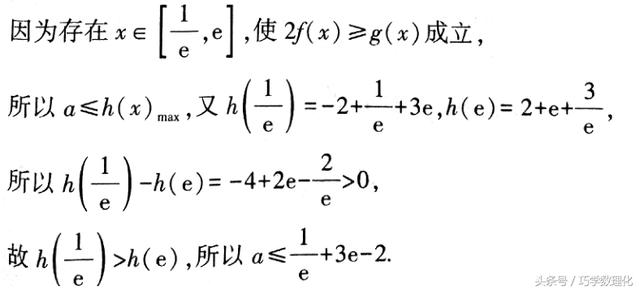
方法四、数形结合法

(1)曲线上的点与直线上点的距离的最值

求与直线不相交的曲线上的点与该直线的距离最值最直观的方法就是“平行切线法”，这种方法是数形结合思想的具体体现．

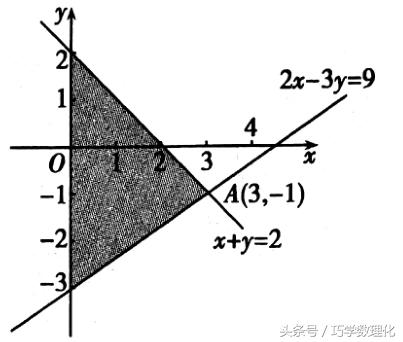
(2)根据求解目标的几何意义求最值

把求解目标的代数表达式赋予其几何意义，就可以把代数问题转化为几何问题、函数问题解决．常见的目标函数的几何意义有：两点连线的斜率、两点间的距离、直线上的点与曲线上的点的距离等．

方法五、构造法

(1)构造函数求最值

对任意实数a，b，当a≠b时，一定存在实数λ，使得a=λb，使用这个知识，可以把某些以比值形式出现的二元不等式转化为一元不等式．

(2)构造模型求最值

根据求解目标的特点，通过联想已知知识构造恰当的模型（如正方形、正方体、函数、数列等）求解最值.