高考数学压轴题 从热点突破计数原理与古典概率

热点一 计数原理与排列与组合

某校的A、B、C、D四位同学准备从三门选修课中各选一门，若要求每门选修课至少有一人选修，且A,B不选修同一门课，则不同的选法有（ ）

A. 36种 B. 72种 C. 30种 D. 66种

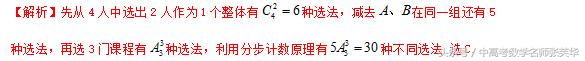
点睛：排列、组合综合应用问题的常见解法：①特殊元素(特殊位置)优先安排法；②合理分类与准确分步；③排列、组合混合问题先选后排法；④相邻问题捆绑法；⑤不相邻问题插空法；⑥定序问题倍缩法；⑦多排问题一排法；⑧“小集团”问题先整体后局部法；⑨构造模型法；⑩正难则反、等价转化法．

在计算排列组合问题时，可能会遇到“分组”问题，要特别注意是平均分组还是不平均分组．可从排列与组合的关系出发，用类比的方法去理解分组问题.

【考向预测】1.两个计数原理是解决排列、组合问题的基本方法，同时又能独立地解决一些简单的计数问题，通常与排列组合问题或概率计算问题综合考查．

2.排列组合问题往往以实际问题为背景，考查排列数、组合数，同时考查分类讨论的思想及解决问题的能力．除了以选择、填空的形式考查，也往往在解答题中与概率相结合进行考查．

热点二 二项式定理

点睛：

（1）对于二项式系数问题，应注意以下几点：

①求二项式所有项的系数和，可采用“特殊值取代法”，通常令字母变量的值为1；

②关于组合恒等式的证明，常采用“构造法”——构造函数或构造同一问题的两种算法；[来源:学_科_网]

③证明不等式时，应注意运用放缩法.

（2）有些三项展开式问题可以变形为二项式问题加以解决；有时也可以通过组合解决，但要注意分类清楚，不重不漏.

（3）对于二项式系数问题，首先要熟记二项式系数的性质，其次要掌握赋值法，赋值法是解决二项式系数问题的一个重要手段.

（4）在二项式定理的应用中，“赋值思想”是一种重要方法，是处理组合数问题、系数问题的经典方法．

（5）在应用通项公式时，要注意公式中，它表示二项展开式的任意项，只要n与r确定，该项就随之确定；a，b的指数和为n且a，b不能随便颠倒位置；

【考向预测】二项式定理中热点是通项公式的应用，利用通项公式求特定项或特定的项的系数，或已知某项，求指数n，求参数的值等．

热点三 古典概型

点睛：古典概型中基本事件的探求方法

(1)枚举法：适合给定的基本事件个数较少且易一一列举出的．[来源:学科网ZXXK]

(2)树状图法：适合于较为复杂的问题中的基本事件的探求，注意在确定基本事件时(x，y)可以看成是有序的，如(1,2)与(2,1)不同．有时也可以看成是无序的，如(1,2)(2,1)相同．

(3)排列组合法：在求一些较复杂的基本事件的个数时，可利用排列或组合的知识．

【考向预测】概率是高考热点之一，特别是古典概型，以互斥事件、对立事件的概率为主．客观题与大题都有可能考查，在大题中更加注重实际背景，考查分析、推理能力.