八年级数学，勾股定理，这个题型通俗又易考！

勾股定理在初中数学的地位是不可撼动的。它揭示了直角三角形三边之间的数量关系，同时也是“数形结合”思想的一个重要考点。所以在学习这个单元的知识之前，一定要先预习一遍课本的知识，并且在课后能花一定时间进行练习巩固。值得注意的是勾股定理通常会结合勾股定理逆定理一并考察！

下面来看一道关于勾股定理的典型题目：

例：如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°，求证：∠A+∠C=180°

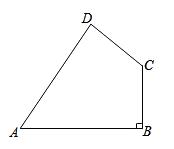
例题图形

分析：由于四边形内角和为360°，那么要求∠A+∠C=180°，在已知∠B=90°的基础上，我们只需求出∠D=90°。这时可以自然的想到用勾股定理逆定理，连接AC，则此题可解。

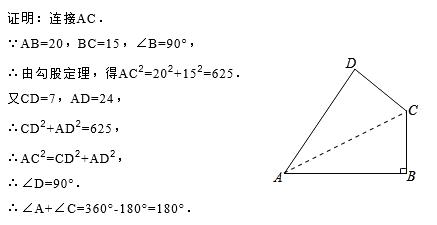
例题解答

变式训练1：如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量∠A=90°，AB=3cm，BC=12cm，CD=13cm，DA=4cm，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

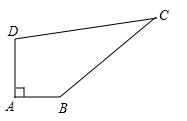
变式训练1图形

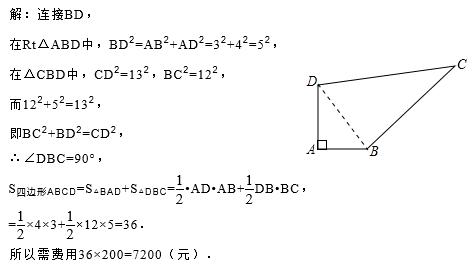
变式训练1答案

变式训练2：如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数。

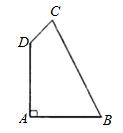
变式训练2图形

变式训练2答案

点评：“勾股数”的记忆对于勾股定理这个单元的计算有着很大的帮助。应该记住一些常见的勾股数：3,4,5；5,12,13；7,24,25；8,15,17等。