八年级数学，正方形轴对称，经典辅助线作法！

八年级是学生两极分化的一个重要时期。就数学这个科目来说，许多七年级还算跟得上的学生，到了八年级就渐渐与大部队脱节了。究其原因，我个人认为和几何知识的增多关系很大。俗话说“几何头，代数尾”，大概意思就是几何入门较难，代数深究不易。从小学到初中，学生的思维其实经历着从“数”到“形”的转化过程。几何的学习不仅要求学生掌握抽象的几何概念，还应理解严谨的几何推理过程。

所以要学好几何，首要目标是严格的训练书写格式，这是几何题目得分的前提。其次就要了解一些常见的辅助线做法。

下面我们看看这一道题目：

例：已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、CD于点M、N，AH⊥MN于点H。

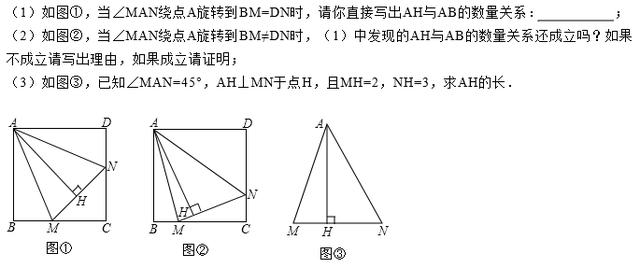
题目

分析：（1）其实严格来说旋转是九年级的知识，但是在此题中旋转只是题目的一个点缀，我们完全可以绕开旋转来用八年级知识解题。

（2）此题的出题符合从特殊到一般再到特殊的出题模式，这种模式是非常热门的，解题时要抓住特殊条件，再用上一步的解题思路来思考下一步的解题方向！

例如第（1）小题的特殊条件就是BM=DN，我们自然会想到利用三角形全等来证明结论。再结合正方形的性质，可得AH=AB。第（2）小题是承上启下的一个题目，我们要继承上一小题三角形全等来解题的思路，思考如何构造全等的三角形。解题的要点是题目中∠MAN=45°的使用！

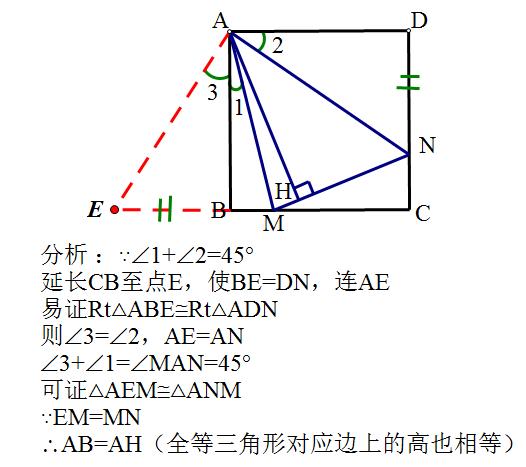
第（3）小题可以利用第（2）小题得到的结论，构造正方形解题。此题对于辅助线的构造要求较高。

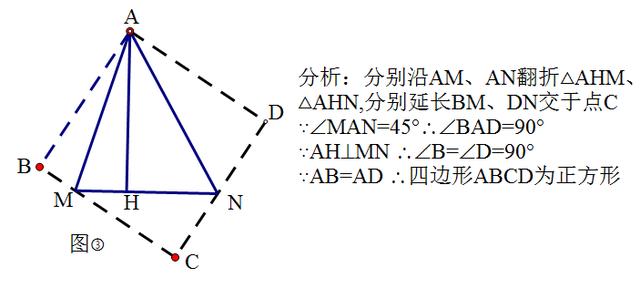
点评：翻折的题目经常需要假设未知数x，构造等量关系求解！