


这里其实可以直接设t=sinx/2,t∈(0,1/2】,由对勾函数性质知函数在(0,1】上为减函数,需要注意的是t本身是有范围的,不要直接写最小值是1或者2,都是特别容易写错的
所谓的对勾函数(双曲函数),是形如
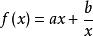
(a>0,b>0)的函数。
由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。


高中数学一题4解,三角函数求最小值,最后一个方法不容易想到



这里其实可以直接设t=sinx/2,t∈(0,1/2】,由对勾函数性质知函数在(0,1】上为减函数,需要注意的是t本身是有范围的,不要直接写最小值是1或者2,都是特别容易写错的
所谓的对勾函数(双曲函数),是形如
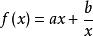
(a>0,b>0)的函数。
由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。


上一篇 : 高中数学重难点归纳:解三角形常考题型有三种类型
下一篇 : 数学干货:高中数学必修二分章节全部知识点
高中7种常用函数图象及4种函数图象变换规则
高中数学必刷题大集合(含答案)
高考数学中外接球你必须掌握的秒杀技巧
 加载中,请稍侯......
加载中,请稍侯......
精彩评论