高考必须掌握的题型：线性规划题型分析总结

老师给大家整理了一下线性规划的内容，这是解析几何的重点。但是这块内容高考只考察5分，一般以选填的情况出现，难度不大。同学们需要的是细心，以及熟练掌握直线的相关性质。

一、已知线性约束条件，探求线性目标关系最值问题

例1、设变量x、y满足约束条件

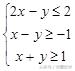
，则

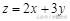
的最大值

为　　　。　

解析：如图1，画出可行域，得在直线2x-y=2与直线x-y=-1的交点A(3,4)处，目标函数z最大值为18

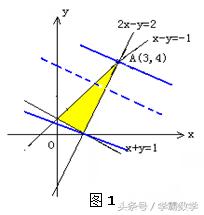
点评：本题主要考查线性规划问题,由线性约束条件画出可行域,然后求出目标函数的最大值.，是一道较为简单的送分题。数形结合是数学思想的重要手段之一。

二、已知线性约束条件，探求非线性目标关系最值问题

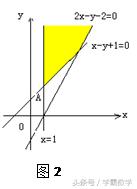
例2、已知

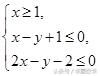
则

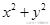
的最小值是_______ .

解析：如图2，只要画出满足约束条件的可行域，而

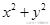
表示可行域内一点到原点的距离的平方。由图易知A（1，2）是满足条件的最优解。

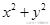
的最小值是为5。

点评：本题属非线性规划最优解问题。求解关键是在挖掘目标关系几何意义的前提下，作出可行域，寻求最优解。

三、约束条件设计参数形式，考查目标函数最值范围问题。

例3、在约束条件

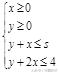
下，当

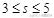
时，目标函数

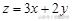
的最大值的变化范围是（）

A.[6,15] B. [7,15] C. [6,8] D.[7,8]

解析：画出可行域如图3所示,当

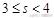
时, 目标函数

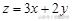
在

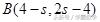
处取得最大值, 即

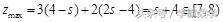
;当

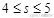
时, 目标函数

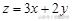
在点

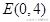
处取得最大值,即

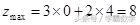
,故

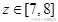
,从而选D;

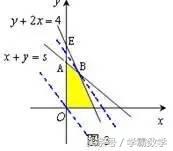
点评：本题设计有新意，作出可行域，寻求最优解条件，然后转化为目标函数Z关于S的函数关系是求解的关键。

四、已知平面区域，逆向考查约束条件。

例4、已知双曲线

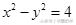
的两条渐近线与直线

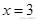
围成一个三

角形区域,表示该区域的不等式组是（）

(A)

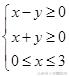
(B)

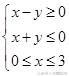
(C)

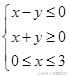
(D)

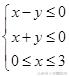
解析：双曲线

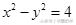
的两条渐近线方程为

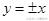
，与直线

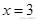
围成一个三角形区域（如图4所示）时有

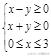
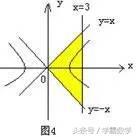
点评：本题考查双曲线的渐近线方程以及线性规划问题。验证法或排除法是最效的方法。

五、已知最优解成立条件，探求目标函数参数范围问题。

例5、已知变量x，y满足约束条件

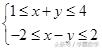
。若目标函数

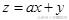
（其中

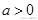
）仅在点(3,1)处取得最大值，则a的取值范

围为_______ 。

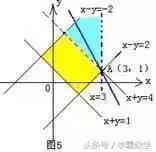
解析：如图5作出可行域，由

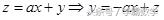
其表示为斜率为-a，纵截距为ｚ的平行直线系, 要使目标函数

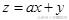
（其中

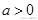
）仅在点(3,1)处取得最大值。则直线

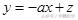
过Ａ点且在直线

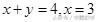
（不含界线）之间。即由-a<-1得a>1,则a的取值范围为

。

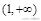
点评：本题通过作出可行域，在挖掘

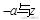
的几何意义的条件

下，借助用数形结合利用各直线间的斜率变化关系，建立满足题设条件的a的不等式组即可求解。求解本题需要较强的基本功，同时对几何动态问题的能力要求较高。

六、设计线性规划，探求平面区域的面积问题

例６、在平面直角坐标系中，不等式组

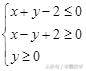
表示的平面区域的面积是（）

(A)

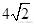
(B)4 (C)

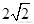
(D)2

解析：如图６，作出可行域，易知不等式组

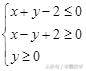
表示的平

面区域是一个三角形。容易求三角形的三个顶点坐标为Ａ（０，２），B(2,0),C(-2,0).于是三角形的面积为：

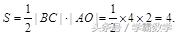
从而选Ｂ。

点评：有关平面区域的面积问题，首先作出可行域，探求平面区域图形的性质；其次利用面积公式整体或部分求解是关键。

七、研究线性规划中的整点最优解问题

例7、某公司招收男职员x名，女职员y名，x和y须满足约束条件

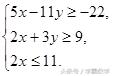
则

的最大值是(A)80 (B) 85 (C) 90 (D)95

解析：如图７，作出可行域，由

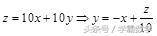
，它表示为斜率为-1，纵截距为

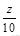
的平行直线系,要使

取得最大值。

当直线

通过

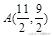
，z取得最大值。因为

，

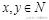
故Ａ点不是最优整数解。于是考虑可行域内Ａ点附近整点Ｂ（５，４），Ｃ（４，４），经检验直线经过Ｂ点时，

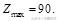
点评：在解决简单线性规划中的最优整数解时，可在去掉限制条件求得的最优解的基础上，调整优解法，通过分类讨论获得最优整数解。