cc518学习网精品学习资料总目录

题型一：三角变换与解三角形的综合问题

方法归纳：

（1）解三角形问题，多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的，其基本步骤是：第一步：定条件，即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向。第二步：定工具，即根据条件与所求合理选择转化的工具，实施边角之间的互化。第三边：求结果

（2）三角变换与解三角形的综合问题要关注三角形中的隐藏条件，如A+B+C=π，sin（A+B）=sinC，cos（A+B）=-cosC，以及在△ABC中，A＞B→sanA＞sinB等。

题型二：解三角形与平面向量结合

解三角形与平面向量综合问题的一般思路

（1）求三角函数值，一般利用向量的相关运算把向量关系转化为三角函数关系。利用同角三角函数关系式及三角函数中常用公式求解

（2）求角时通常由向量转化为三角函数问题，先求值再求角。

（3）解决与向量有关的三角函数问题的思想方法是转化与化归的数学思想，即通过向量的相关运算把问题转化为三角函数问题。

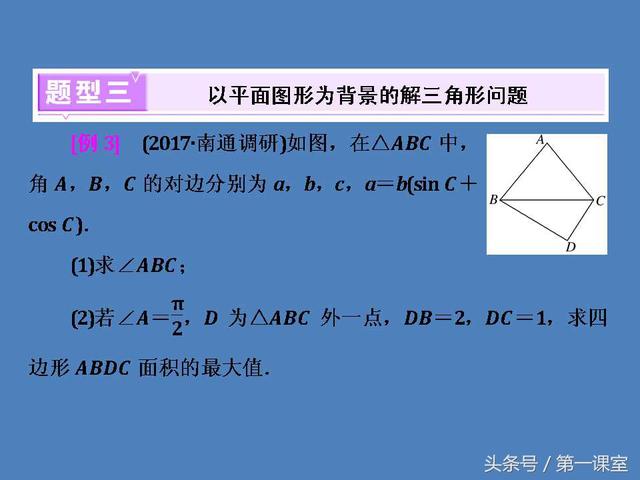
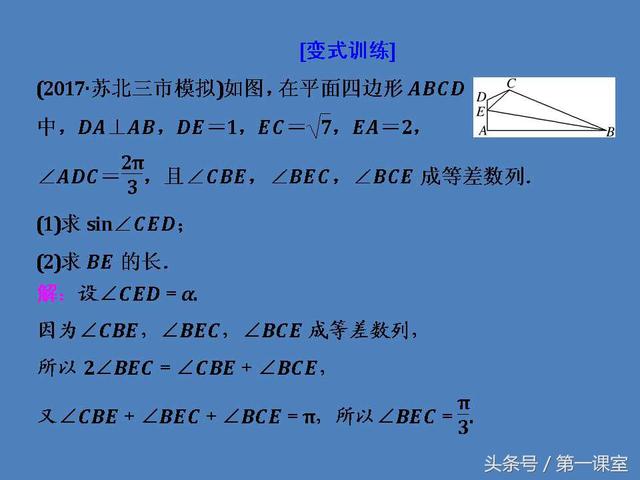
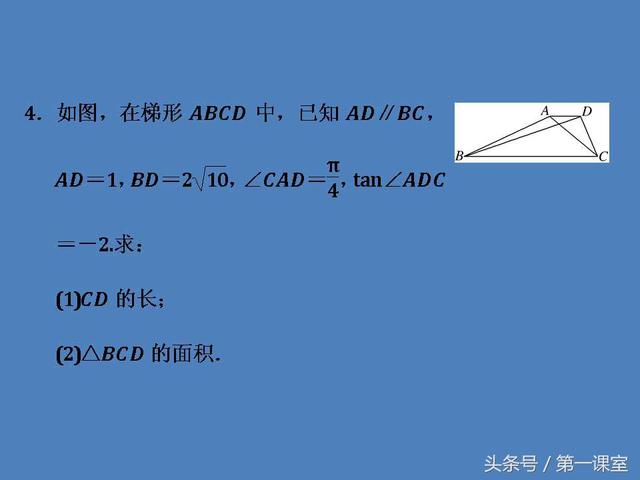
题型三：以平面图形为背景的解三角形问题

以平面图形为背景的解三角形问题的一般思路

（1）建联系：在平面几何图形中求相关的几何量时，需寻找各个三角形之间的联系，交叉使用公共条件，通过公共条件形成等式，常常将所涉及的已知几何量与所求几何集中在某一个三角形。

（2）用定理：①“已知两角和一边”或“已知两边和其中一边的对角”应采取正弦定理②“已知两边和这两边的夹角”或“已知三角形的三边”应采取余弦定理